题目内容
一质量为m的小球,用长为l的轻绳悬于O点,小球在水平力F作用下,从平衡位置P点缓慢地移到Q点,此时绳与竖直夹角为θ,如图5-3,则力F所做的功为( )
图5-3
A.mglcosθ B.Flsinθ C.mgl(1-cosθ) D.Flθ
解析:方法一:分析小球从P到Q过程中受力情况:重力、绳的拉力和水平力F.
从P到Q应用动能定理∑W=ΔEk.
因为绳的拉力不做功,重力做负功WG=-mgh=-mgl(1-cosθ),球缓慢移动,速度可视为零,
故各点处动能为零,设水平力的功为WF,则WF-mgl(1-cosθ)=0,即WF=mgl(1-cosθ).
方法二:应用能量转化与守恒定律,小球从P到Q的过程中,重力势能增加了mgl(1-cosθ),动能没有变化,即总能量增加了mgl(1-cosθ),这个能量的增加恰好是力F对小球做的功,即W=mgl(1-cosθ).
答案:C

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
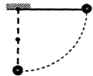 一质量为m的小球,用长L为的细线悬挂于O点,在O点正下方L/2处钉有钉,把悬线沿水平方向拉直后无初速释放,当悬线碰到钉子瞬间( )
一质量为m的小球,用长L为的细线悬挂于O点,在O点正下方L/2处钉有钉,把悬线沿水平方向拉直后无初速释放,当悬线碰到钉子瞬间( )| A、小球的线速度突然变小 | B、小球的角速度变大 | C、小球的向心加速度突然变大 | D、悬线拉力不变 |
 一质量为m的小球,用长为L的轻绳悬挂在 O点,小球在水平恒力F作用下,从静止开始由平衡位置P点移动到Q点,此时绳与竖直方向的偏角为θ如图所示,则力F所做的功为( )
一质量为m的小球,用长为L的轻绳悬挂在 O点,小球在水平恒力F作用下,从静止开始由平衡位置P点移动到Q点,此时绳与竖直方向的偏角为θ如图所示,则力F所做的功为( ) 一质量为m的小球A用轻绳系于O点,如果给小球一个初速度使其在竖直平面内做圆周运动,某时刻小球A运动的圆轨道的水平直径的右端点时,如图所示位置,其加速度大小为
一质量为m的小球A用轻绳系于O点,如果给小球一个初速度使其在竖直平面内做圆周运动,某时刻小球A运动的圆轨道的水平直径的右端点时,如图所示位置,其加速度大小为 一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平F作用下,从静止由最底位置P点拉到Q点,.如图所示,此时悬线与竖直方向夹角为θ,①当F为恒力时,拉力F做功为W1,②当F使小球缓慢上升时,拉力F做功为W2( )
一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平F作用下,从静止由最底位置P点拉到Q点,.如图所示,此时悬线与竖直方向夹角为θ,①当F为恒力时,拉力F做功为W1,②当F使小球缓慢上升时,拉力F做功为W2( ) 一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示.则水平力F所做的功为
一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如图所示.则水平力F所做的功为