题目内容
（2006?广东）宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用．已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行．设每个星体的质量均为m．
（1）试求第一种形式下，星体运动的线速度和周期．
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？
（1）试求第一种形式下，星体运动的线速度和周期．
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？
分析：明确研究对象，对研究对象受力分析，找到做圆周运动所需向心力的来源．
解答：解：（1）在第一种形式下：三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；
其中边上的一颗星受中央星和另一颗边上星的万有引力提供向心力．
+
=m
v=
T=
=4πR
①
（2）另一种形式是三颗星位于等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行，
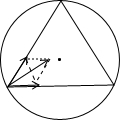
由万有引力定律和牛顿第二定律得：
2
cos30°=m
(
)2 ②
有①②解得：l=
R．
答：（1）试求第一种形式下，星体运动的线速度为
，周期为4πR
．
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为
R．
其中边上的一颗星受中央星和另一颗边上星的万有引力提供向心力．
| Gm2 |
| R2 |
| Gm2 |
| (2R)2 |
| v2 |
| R |
v=
|
T=
| 2πR |
| v |
|
（2）另一种形式是三颗星位于等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行，
由万有引力定律和牛顿第二定律得：
2
| Gmm |
| l2 |
| l |
| 2cos30° |
| 2π |
| T |
有①②解得：l=
| 3 |
| ||
答：（1）试求第一种形式下，星体运动的线速度为
|
|
（2）假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为
| 3 |
| ||
点评：万有引力定律和牛顿第二定律是力学的重点，在本题中有些同学找不出什么力提供向心力，关键在于进行正确受力分析．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
（2006?广东）两束不同频率的单色光a、b从空气射入水中，发生了如图所示的折射现象（α＞β）．下列结论中正确的是（ ）
（2006?广东模拟）一个允许通过最大电流为2A的电源和一个滑动变阻器，接成如下图甲所示的电路．滑动变阻器最大阻值为R0=22Ω，电源路端电压U随外电阻R变化的规律如下图乙所示，图中U=12V的直线为图线的渐近线．试求：
（2006?松江区二模）1998年6月3日凌晨，举世瞩目的美国“发现号”航天飞机从肯尼迪航天中心顺利发射升空，阿尔法磁谱仪搭乘“发现号”航天飞机进入太空，寻找宇宙中可能存在的反物质，只要磁谱仪能发现一个反氦核，就能推断有反星球的存在，那将极大推动宇宙科学的发展，阿尔法磁谱仪的核心部分是由我国科学家和工程师经4年努力研制的永磁体，直径1.2m，长0.8m，重2×103kg，它的作用是产生一个很强的磁场，当宇宙中的带电粒子穿过这个磁场时，记录下有关数据和偏转情况，再用电子计算机进行数据处理，从而确定是否有反质子、反氦核乃至反碳核存在，如图为磁谱仪的截面示意图，永磁体产生方向垂直纸面向里的磁场，图中“×”表示磁场方向，a、b、c分别为宇宙的三个粒子，根据偏转可以判断a、b、c的电性顺序是（ ）