题目内容
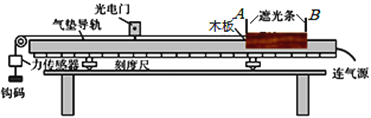
【题目】如图(a)所示，可视为质点的物块质量为m=2kg，置于水平地面上的A点，物块与水平地面间的动摩擦因数μ=0.25。在水平向右的力F作用下物块由静止开始运动，由A运动到B的过程中力F随位移x变化关系如图(b)所示，到达斜面底端B点后撤去力F，物块冲上足够长的光滑斜面。其中AB段长为L=5m，g取10m/s2。问：
(1)由A运动到B的过程中，物块克服摩擦力所做的功是多少？
(2)物块由A运动到B所用的时间是多少？
(3)不计物块在B处的动能损失，物块沿斜面上滑的最大高度是多少？
【答案】(1)25J；(2)1.5s；(3)
【解析】
(1)由
运动到
的过程中，设物块受滑动摩擦力
的作用，物块克服摩擦力做功
，则有：
(2)由图像可知在
内，则有：
故物块做初速度为零的匀加速直线运动，由牛顿第二定律可得：
可得：
由匀变速直线运动公式
可得：
到达点时的速度：
在
内，则有：
故物块做匀速直线运动，以
的速度做匀速运动：
因此，物块由运动到所用的时间：
(3)因为斜面光滑，物块在斜面上运动时机械能守恒。由机械能守恒定律可得：
解得：
练习册系列答案
相关题目
