题目内容
质量为m的探月航天器在接近月球表面的轨道上飞行，视为匀速圆周运动，已知月球质量为M，月球半径为R，月球对航天器的万有引力为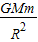
，不考虑月球自转，则航天器的（ ）A．线速度v=
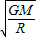
B．角速度ω=
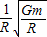
C．运行周期T=πR
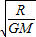
D．向心加速度an=
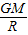
【答案】分析：研究月航天器绕月球做匀速圆周运动，根据万有引力提供向心力，列出等式求出问题．
向心力的公式选取要根据题目提供的已知物理量或所要求解的物理量选取应用．
解答：解：根据万有引力提供卫星做圆周运动的向心力：
F=G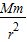
=
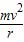=mω2r=m
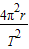=ma得：
A、航天器的线速度v=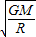
，故A正确
B、航天器的角速度ω=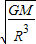
，故B错误
C、运行周期T=2πR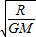
，故C错误
D、航天器的向心加速度a=G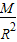
，故D错误
故选A．
点评：解决该题关键要根据万有引力提供卫星做圆周运动的向心力进行卫星加速度、线速度、周期和角速度的求解．
向心力的公式选取要根据题目提供的已知物理量或所要求解的物理量选取应用．
解答：解：根据万有引力提供卫星做圆周运动的向心力：
F=G
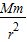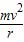==mω2r=m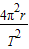=ma得：A、航天器的线速度v=
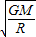，故A正确B、航天器的角速度ω=
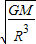，故B错误C、运行周期T=2πR
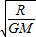，故C错误D、航天器的向心加速度a=G
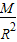，故D错误故选A．
点评：解决该题关键要根据万有引力提供卫星做圆周运动的向心力进行卫星加速度、线速度、周期和角速度的求解．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
（2012?闵行区三模）（A） 如图，质量为M=3kg的木板放在光滑水平面上，质量为m=1kg的物块在木板上，它们之间有摩擦，木板足够长，两者都以v=4m/s的初速度向相反方向运动，当木板的速度为v1=2.4m/s时，物块的速度是质量为m的探月航天器在离月球表面高度为R的轨道上飞行，其运动视为匀速圆周运动．已知月球质量为M，月球半径也为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的（ ）
A、角速度ω=
| ||||
B、线速度v=
| ||||
C、运行周期T=2π
| ||||
D、向心加速度a=
|