题目内容
3. 如图所示的直角坐标系中,从直线x=-2l0到y轴区域存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界从A(-2l0,-l0)点到C(-2l0,0)点的区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起,A点到C点间的粒子依次连续以相同速度v0沿x轴正方向射入电场.从A点射入的粒子恰好从y轴上的A′(0,l0)点沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.
如图所示的直角坐标系中,从直线x=-2l0到y轴区域存在两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界从A(-2l0,-l0)点到C(-2l0,0)点的区域内,连续分布着电量为+q、质量为m的粒子.从某时刻起,A点到C点间的粒子依次连续以相同速度v0沿x轴正方向射入电场.从A点射入的粒子恰好从y轴上的A′(0,l0)点沿x轴正方向射出电场,其轨迹如图所示.不计粒子的重力及它们间的相互作用.(1)匀强电场的电场强度;
(2)在A、C间还有哪些位置的粒子,通过电场后也能沿x轴正方向运动?
(3)为便于粒子收集,可在直线x=2l0上的某点为圆心的圆形区域内,加一垂直于xOy平面向里的匀强磁场,使得沿x轴正方向射出电场的粒子经磁场偏转后,都能通过直线x=2l0与圆形磁场边界的一个交点.则磁场区域的最小半径是多大?相应的磁感应强度B是多大?
分析 (1)将带电粒子的运用沿水平和竖直方向正交分解,水平方向做匀速直线运动,竖直方向在x轴上下方都做匀变速直线运动,根据牛顿第二定律和运动学公式列式分析;
(2)先画出运动的一般轨迹,要使粒子通过电场后能沿x轴正方向运动,其第一次到达x轴的水平分位移的2n倍等于2l0,根据牛顿第二定律和运动学公式列式分析即可;
(3)先画出各个粒子的运动轨迹,然后根据题意确定磁场范围,最后根据洛伦兹力提供向心力求解磁感应强度.
解答 解:(1)设从A点射入的粒子由A点到A'点的运动时间为t,根据运动轨迹的对成称性,
x方向有:2l0=v0t
得:t=$\frac{2{l}_{0}}{{v}_{0}}$…①
y方向有:l0=$\frac{qE}{2m}$($\frac{t}{2}$)2…②
解得:E=$\frac{2m{v}_{0}^{2}}{q{l}_{0}}$…③
即从AC间入射的粒子穿越电场区域的时间t为 $\frac{2{l}_{0}}{{v}_{0}}$,匀强电场的电场强度E的大小为 $\frac{2m{v}_{0}^{2}}{q{l}_{0}}$.
(2)设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向,粒子第一次到达x轴用时△t,水平分位移△x,
则有:△x=v0△t…④
△y=$\frac{qE}{2m}$(△t)2…⑤
要粒子从电场中射出时速度方向也沿x轴正方向,必须满足条件为:2l0=n•2△x(n=1,2,3…)…⑥
联立③④⑤⑥解得:△y=$\frac{1}{{n}^{2}}$l0…⑦
故粒子从电场中射出时速度方向也沿x轴正方向,必须是在AC间纵坐标为: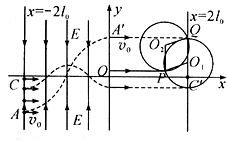 y=(-1)n•$\frac{1}{{n}^{2}}$l0,(n=1,2,3…)…⑧
y=(-1)n•$\frac{1}{{n}^{2}}$l0,(n=1,2,3…)…⑧
(3)当n=1时,粒子射出的坐标为y1=l0…⑨
当n=2时,粒子射出的坐标为y2=-$\frac{1}{4}$l0…⑩
当n≥3时,沿x轴正方向射出的粒子分布在y1到y2之间(如图所示).
y1、y2之间距离为 L=y1-y2=$\frac{5}{4}$l0…(11)
所以,磁场圆O1的最小半径 R=$\frac{L}{2}$=$\frac{5}{8}{l}_{0}$…(12)
若使粒子经磁场后汇集于直线x=2l0与圆形磁场边界的一个交点,分析知此点只能是答图中的Q点,且粒子在磁场中做圆周运动的半径等于磁场区域圆半径.
由 qv0B=m$\frac{{v}_{0}^{2}}{R}$…(13)
联立(12)、(13)得:B=$\frac{8m{v}_{0}}{5q{l}_{0}}$…(14)
即磁场区域的最小半径是$\frac{5}{8}{l}_{0}$,相应的磁感应强度B是$\frac{8m{v}_{0}}{5q{l}_{0}}$.
答:(1)匀强电场的电场强度为$\frac{2m{v}_{0}^{2}}{q{l}_{0}}$;
(2)在A、C间纵坐标为:y=(-1)n•$\frac{1}{{n}^{2}}$l0,(n=1,2,3…)的粒子,通过电场后也能沿x轴正方向运动.
(3)磁场区域的最小半径是$\frac{5}{8}{l}_{0}$,相应的磁感应强度B是$\frac{8m{v}_{0}}{5q{l}_{0}}$.
点评 本题关键是将粒子的运动沿着水平方向和竖直方向正交分解,然后根据牛顿运动定律和运动学公式列式分析求解;解题过程中要画出轨迹图分析,特别是第三小题,要画出准确的圆轨迹图分析才能有助与问题的解决.

 名校课堂系列答案
名校课堂系列答案 2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里远的太阳与地球引力平衡点--拉格朗日L2点的环绕轨道.拉格朗日L2点位于太阳与地球连线的延长线上,“嫦娥二号”位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,下列说法正确的是( )
2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里远的太阳与地球引力平衡点--拉格朗日L2点的环绕轨道.拉格朗日L2点位于太阳与地球连线的延长线上,“嫦娥二号”位于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,下列说法正确的是( )| A. | “嫦娥二号”在该点处于平衡状态 | |
| B. | “嫦娥二号”需要的向心力仅由太阳提供 | |
| C. | “嫦娥二号”运动的周期等于地球的周期 | |
| D. | “嫦娥二号”如果想到离太阳更远的深空进行探测必须继续加速 |
 一列简谐横波沿x轴传播,周期为T,t=0时的波形如图所示,此时平衡处于x=3m处的质点正在向上运动,若a,b两质点平衡位置的坐标分别为xa=2.5m和xb=5.5m,则( )
一列简谐横波沿x轴传播,周期为T,t=0时的波形如图所示,此时平衡处于x=3m处的质点正在向上运动,若a,b两质点平衡位置的坐标分别为xa=2.5m和xb=5.5m,则( )| A. | 此列波沿x轴负方向传播 | |
| B. | 当t=$\frac{T}{4}$时,a质点正在向y轴负方向运动 | |
| C. | 当t=$\frac{3T}{4}$时,b质点正在向y轴负方向运动 | |
| D. | 当a质点处在波峰时,b质点恰在波谷 |
| A. | 物体做曲线运动时,它的速度一定变化 | |
| B. | 物体受到一个不变的恒力作用时,也可能做曲线运动 | |
| C. | 所有做曲线运动的物体,所受合外力方向与速度方向肯定不在一条直线上 | |
| D. | 所有做曲线运动的物体,所受合外力方向与速度方向肯定在一条直线上 |

 如图所示,在离心机的光滑水平横杆上穿有两个质量分别为2m和m的小球A和B,A、B间用劲度系数为k的轻质弹簧连接,弹簧的自然长度为L,当离心机以角速度ω转动时,欲使A、B两球仍能相对横杆静止而不碰到两侧挡板,已知两板间的距离为3L,求转速ω的最大值.
如图所示,在离心机的光滑水平横杆上穿有两个质量分别为2m和m的小球A和B,A、B间用劲度系数为k的轻质弹簧连接,弹簧的自然长度为L,当离心机以角速度ω转动时,欲使A、B两球仍能相对横杆静止而不碰到两侧挡板,已知两板间的距离为3L,求转速ω的最大值.
 质量为m的物体静置于倾角为θ的斜面上,如图所示,用水平力F使斜面体向左以速度V匀速移动距离S,物体与斜面体保持相对静止,则在这一过程中,斜面体对物体的摩擦力做功为-mgs•sinθ•cosθ,斜面体对物体的支持力的功率为mgvsinθ•cosθ.
质量为m的物体静置于倾角为θ的斜面上,如图所示,用水平力F使斜面体向左以速度V匀速移动距离S,物体与斜面体保持相对静止,则在这一过程中,斜面体对物体的摩擦力做功为-mgs•sinθ•cosθ,斜面体对物体的支持力的功率为mgvsinθ•cosθ.