题目内容
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2 m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为![]() 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10 m/s2.
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10 m/s2.

(1)最终A、B、C的速度是多少?
(2)要使C完全离开B并不脱离木板A,每块木板的长度应满足什么条件?
解析:
|
(1)一开始A与水平地面之间的滑动摩擦力f1=μmg,A在F的作用下向右加速运动. 由动能定理得 (F-f1)s= A、B两木块的碰撞瞬间,内力的冲量远大于外力的冲量,由动量守恒定律得mv1=(m+m)v2 ② 碰撞结束后到三个物体达到共同速度的相互作用过程中,设AB整体、C向前移动的位移分别为S1、s2,受滑动摩擦力分别为f2=3μmg、f3=μmg, 选三个物体构成的整体为研究对象,外力之和为零,则 2mv2=(2m+m)v3 ③ 解①②③得v3= 所以最终A、B、C的速度是 (2)对于AB整体 (F-f2)s1-f3s1= 对于C f3 s2= C相对于AB的位移为S3,由几何关系得 2L+S2+S3=S1+2L ⑦ ②③④⑤⑥解得S3= 要使C刚好完全离开B(即AC对齐)C相对于A的位移 要使C不脱离木板A则 解得 要使C完全离开B并不脱离木板A,每块木板的长度应满足: |

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为 如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
如图所示,三块木板A、B、C的质量均为m,长度均为L.A、B置于水平地面上,它们的间距s=2m.C置于B板的上端并对齐.A、B、C之间及A、B与地面之间的动摩擦因数均为μ=0.2,最大静摩擦力可以认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给A施加一个水平向右,大小为
 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取l0m/s2.求:
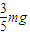 的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.
的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起,最终C没有脱离A板,g取10m/s2.