题目内容
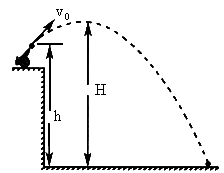
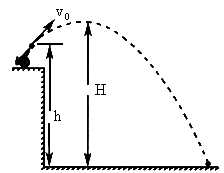
如图所示,一门大炮置于一山崖边,炮口距地面高度为h=60m,以45°的仰角发射一颗炮弹,炮弹的初速度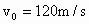 ,求:
,求:
(1)炮弹所达到的最大高度H;
(2)炮弹落地的时间和速度;
(3)炮弹的水平射程(忽略空气阻力,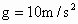 ).
).
答案:略
解析:
解析:
|
将初速度分解得,在竖直方向的分速度为
(1) 竖直方向上炮弹做竖直上抛运动
(2) 由竖直上抛运动的公式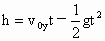 得 得
解得
竖直分速度:
水平分速度: 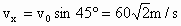 . .
合速度大小: 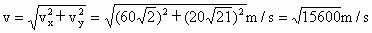 ; ;
合速度方向: 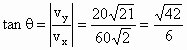 (q
为速度与水平方向的夹角), (q
为速度与水平方向的夹角),
(3) 水平射程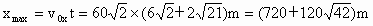 . .
炮弹离开炮口后做斜抛运动,斜抛运动可以分解成水平方向的匀速直线运动和竖直方向的上抛运动.当炮弹达到最高点时竖直分速度减到零.根据这一特点可以求出射高;落地时在竖直方向出现了负位移,将此负位移代入上抛运动公式可求出时间及竖直方向的分速度,再与水平分速度合成即得落地时的速度;水平射程是落地前这段时间内水平方向匀速直线运动的位移. 本题由于抛出点和落地点不在同一水平高度,所以不能简单套用斜抛运动的公式,以免出现错误. 斜抛运动的处理方法就是将它分解,分解成水平方向的匀速直线运动和竖直方向的竖直上抛运动.物体在抛出点上方时竖直方向的分位移为正,物体在抛出点下方则竖直方向的分位移为负值,这样首先确定运动时间,再处理水平方向的射程. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,物体m静置于一斜面上,斜面固定,若斜面的倾角稍微增加一些,物体m仍然静止在斜面上,则 ( ) 
| A.斜面对物体的支持力变大 | B.斜面对物体的摩擦力变大 |
| C.斜面对物体的摩擦力变小 | D.物体所受的合外力变大 |
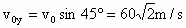
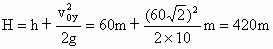
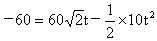
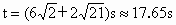
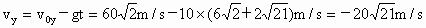

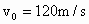 ,求:
,求: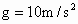 ).
).