题目内容
9. 某兴趣小组测量小物块与水平面之间的动摩擦因数和弹簧压缩后弹性势能大小的装置如图所示.弹簧左端固定在挡板上,右端被带有挡光条的小物块压至C处.现由静止释放小物块,小物块与弹簧分离后通过P处光电计时器的光电门,最终停在水平面上某点B.已知挡光条的宽度为d,当地重力加速度为g.
某兴趣小组测量小物块与水平面之间的动摩擦因数和弹簧压缩后弹性势能大小的装置如图所示.弹簧左端固定在挡板上,右端被带有挡光条的小物块压至C处.现由静止释放小物块,小物块与弹簧分离后通过P处光电计时器的光电门,最终停在水平面上某点B.已知挡光条的宽度为d,当地重力加速度为g.(1)现测得挡光条通过光电门的时间为t,小物块停止处到光电门的距离为x,则小物块通过光电门处的速度v=$\frac{d}{t}$,小物块与水平面间的动摩擦因数μ=$\frac{{d}^{2}}{2gx{t}^{2}}$(用g、d、t、x表示).
(2)若小物块质量为m,释放处C到光电门P的距离为x0,则小物块释放瞬间弹簧的弹性势能EP=$\frac{m{d}^{2}({x}_{0}+x)}{2x{t}^{2}}$(用m、d、t、x、x0表示).
分析 (1)瞬时速度等于平均速度,根据动能定理求得摩擦因数;
(2)整个过程中利用动能定理求得弹簧的弹性势能.
解答 解:(1)利用平均速度可知通过光电门的速度为:$v=\frac{d}{t}$
根据动能定理可知:$-μmgx=0-\frac{1}{2}m{v}^{2}$,
解得:μ=$\frac{{d}^{2}}{2gx{t}^{2}}$
(2)从C到静止利用动能定理可知:
EP-μmg(x0+x)=0-0
解得:EP=$\frac{m{d}^{2}({x}_{0}+x)}{2x{t}^{2}}$
故答案为:(1)$\frac{d}{t}$,$\frac{{d}^{2}}{2gx{t}^{2}}$;(2)$\frac{m{d}^{2}({x}_{0}+x)}{2x{t}^{2}}$
点评 本题主要考查了动能定理,抓住过程即可求得,明确瞬时速度等于平均速度即可判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
 如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )
如图,质量为m的带电小球A用绝缘细线悬挂于O点,处于静止状态.施加一水平向右的匀强电场后,A向右摆动,摆动的最大角度为60°,则A受到的电场力大小为( )| A. | $\frac{mg}{2}$ | B. | $\frac{\sqrt{3}mg}{3}$ | C. | mg | D. | $\sqrt{3}$mg |
18.下列有关布朗运动的说法正确的是( )
| A. | 悬浮颗粒越小,布朗运动越显著 | |
| B. | 悬浮颗粒越大,布朗运动越显著 | |
| C. | 液体的温度越高,布朗运动越显著,所以布朗运动又叫热运动 | |
| D. | 液体的温度高低对布朗运动不产生影响 |
19. 某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )
某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )
 某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )
某人乘电梯下楼,在竖直下降的过程中,电梯速度的平方v2与下降的位移x的关系如图所示,则人对地板的压力( )| A. | x=1m时大于人的重力 | B. | x=11m时大于人的重力 | ||
| C. | x=21m时大于人的重力 | D. | x=21m时等于人的重力 |

 如图示,光滑的U型导轨形成一个倾角为30°的斜面,导轨的水平间距为l=10cm,在斜面上有垂直斜面向上的匀强磁场,磁感应强度B=20T,一质量为m=2kg的导体棒在导轨上由静止释放,导体棒的电阻R=2Ω,导轨电阻不计,当小球沿斜面下滑S=6m时,导体棒获得最大速度.求
如图示,光滑的U型导轨形成一个倾角为30°的斜面,导轨的水平间距为l=10cm,在斜面上有垂直斜面向上的匀强磁场,磁感应强度B=20T,一质量为m=2kg的导体棒在导轨上由静止释放,导体棒的电阻R=2Ω,导轨电阻不计,当小球沿斜面下滑S=6m时,导体棒获得最大速度.求
 如图所示,在“探究力的合成的平行四边形定则”实验中,橡皮条一端固定于A点.
如图所示,在“探究力的合成的平行四边形定则”实验中,橡皮条一端固定于A点.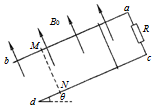 如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,ab、cd为间距d=1m的光滑倾斜金属导轨,与水平面的夹角θ=37°,导轨电阻不计,a、c间连接电阻R=2.4Ω.空间存在磁感应强度B0=2T的匀强磁场,方向垂直于导轨平面向上.将一根金属棒放置在导轨上距ac为x0=0.5m处,其质量m=0.5kg,电阻r=0.8Ω.现将金属棒由静止释放,金属棒沿导轨向下运动过程中始终与ac平行且与导轨接触良好.已知当金属棒从初始位置向下滑行x=1.6m到达MN处时已经达到稳定速度,金属导轨足够长,sin37°=0.6,cos37°=0.8,g取10m/s2.求: