题目内容
如图所示，用一根长为l且不可伸长的细线，将质量均为m的两个小球A和B连接后放在光滑的水平桌面上，并使之相距l/2．现沿垂直于A、B连线的方向，给小球B一水平初速度v0，使之运动起来，求：在A球固定和A球可自由移动两种情况下，由A、B两球组成的系统最终损失的动能之比．
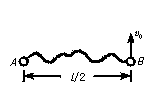
答案：
解析：
解析：
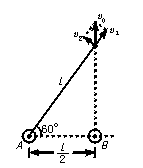
设计意图：本题考查在不同情况下讨论系统动量是否守恒问题以及能量守恒问题．同时考查了运动的合成分解． 解析：在细绳伸直前的一瞬间，将小球B的速度分解如图所示：
(1)A球固定： 在细线伸直后的瞬间，由于细线不可伸长，沿细线向外的分速度v1=v0sin60°= (2)A球不固定： 在细线伸直后的瞬间，沿着细线的方向，两球有共同速度v′，由动量守恒定律得：
故： 易错点：小球A、B通过细线相互作用时，由于细线的张力与分速度v2垂直，不能改变v2的大小，与之对应的动能也就没有损失．在此分析不清易造成错解． 答案：ΔE1/ΔE2=2/1 |
v0立即变为0．系统损失的动能ΔE1=
．
=
即解得：
=
．系统损失的动能Δ
=
．
=
练习册系列答案
相关题目
（2008?江苏模拟）如图所示，用一根长为L的细绳一端固定在O点，另一端悬挂质量为m的小球A，为使细绳与竖直方向夹30°角且绷紧，小球A处于静止，则需对小球施加的最小力等于（ ）
如图所示，用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点连接并悬挂于O点，悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场，且d0《L．先将线框拉开到如图所示位置，松手后让线框进入磁场，忽略空气阻力和摩擦．下列说法正确的是（ ）
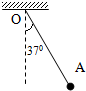如图所示，用一根长为L的细绳一端固定在O点，另一端悬挂质量为m的小球A，为使细绳与竖直方向夹370角且小球A保持静止状态，则需对小球施加第三个力，下列说法（ ）A、等于
| ||
B、等于
| ||
| C、等于mg时，一定竖直向上 | ||
| D、以上说法均不正确 |
如图所示，用一根长为L质量不计的细杆与一个上弧长为l0、下弧长为d0的金属线框的中点联结并悬挂于O点，悬点正下方存在一个上弧长为2l0、下弧长为2d0的方向垂直纸面向里的匀强磁场，且d0＜＜L，先将线框拉开到如图所示位置，松手后让线框进入磁场，忽略空气阻力和摩擦．下列说法正确的是（ ）| A、金属线框进入磁场时感应电流的方向为a→d→c→b→a | B、金属线框离开磁场时感应电流的方向为a→d→c→b→a | C、金属线框dc边进入磁场与ab边离开磁场的速度大小总是相等 | D、金属线框最终将停在最低点 |
