��Ŀ����
��ͼ��ʾ����ֱ���õ�����ƽ�н����峤L��������ҲΪL��������г�ǿΪE����ǿ�糡���糡����������֮�䣩���Ҽ�����¶˸պô���һ�н���ǿ�ų��ı߽磨������ʾ���ϣ��ñ߽���ˮƽ��45��нǣ��߽��������д�ֱֽ���������ǿ�ų���һ����Ϊm������Ϊe�ĵ���������������е�Ӿ�ֹ��ʼ���ڵ糡�������¼��������˶��������Ҽ�������С������ǿ�ų�����
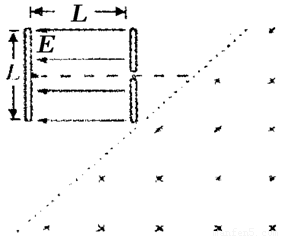
��1���ӵ��ӿ�ʼ�˶���������ǿ�ų������ʱ�䣻
��2����ǿ�ų��ĴŸ�Ӧǿ��BӦ����ʲô���������ܱ�֤���ӴӴų��������ܴ�Խƽ�н������ĵ糡����
���𰸡�
��
��������
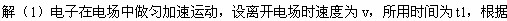

t=t1+t2=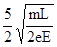 (3��)
(3��)
��2�������ڴų�����Բ���˶���x��3��4�ܴӴų�����ʱ���ٶ�Ӧ����ֱ�����ڵ糡������ƽ���˶�������Ӵ�Խ�糡����ʱ��Ϊt3��ƫת����Ϊx����L��vt3��(2��)
x=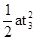 (2��)
(2��)
Ϊ��֤���ӴӴų��������ܽ���糡���ܴӵ糡�г����������ڴų����˶��İ뾶RӦ����
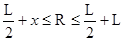 ��2�֣�
��2�֣�
�����ڴų����˶�����뾶��R��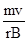 ��2�֣�
��2�֣�
�����Ϲ�ʽ�ɵã�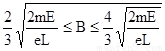 ��4�֣�
��4�֣�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��ʾ����ֱ���õĹ⻬Բ��������һ����Ϊm��С��С����ߵ�ʱ���ٶ�Ϊ
��ͼ��ʾ����ֱ���õĹ⻬Բ��������һ����Ϊm��С��С����ߵ�ʱ���ٶ�Ϊ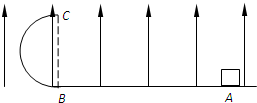 ��ͼ��ʾ����ֱ���õİ�Բ�ξ�Ե����뾶ΪR���¶����Եˮƽ��ƽ�����ӣ�����װ�ô��ڷ�����ֱ���ϵ���ǿ�糡E�У�һ����Ϊm��������Ϊ+q����飨����Ϊ�ʵ㣩����ˮƽ���ϵ�A���Գ��ٶ�v0ˮƽ�����˶����ذ�Բ�ι��ǡ��ͨ����ߵ�C����ǿ��С
��ͼ��ʾ����ֱ���õİ�Բ�ξ�Ե����뾶ΪR���¶����Եˮƽ��ƽ�����ӣ�����װ�ô��ڷ�����ֱ���ϵ���ǿ�糡E�У�һ����Ϊm��������Ϊ+q����飨����Ϊ�ʵ㣩����ˮƽ���ϵ�A���Գ��ٶ�v0ˮƽ�����˶����ذ�Բ�ι��ǡ��ͨ����ߵ�C����ǿ��С ��ͼ��ʾ����ֱ���õ��ᵯ��һ�˹̶��ڵ����ϣ���һ����б����P�̶���P��б�ŵĹ̶�����MN�Ӵ��Ҵ��ھ�ֹ״̬����б����P�˿��ܵ������ĸ��������ǣ�������
��ͼ��ʾ����ֱ���õ��ᵯ��һ�˹̶��ڵ����ϣ���һ����б����P�̶���P��б�ŵĹ̶�����MN�Ӵ��Ҵ��ھ�ֹ״̬����б����P�˿��ܵ������ĸ��������ǣ�������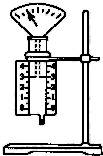 ����ѡ��3-3
����ѡ��3-3 ��ͼ��ʾ����ֱ���õ�U�ε����ΪL���϶˴��е���R�����ർ�岿�ֵĵ��趼���Բ��ƣ����Ÿ�Ӧǿ��ΪB����ǿ�ų�����ֱ��ֽ�����⣮������ab������Ϊm���뵼��Ӵ����ã�����Ħ�����Ӿ�ֹ�ͷź�ab����ˮƽ���»�������
��ͼ��ʾ����ֱ���õ�U�ε����ΪL���϶˴��е���R�����ർ�岿�ֵĵ��趼���Բ��ƣ����Ÿ�Ӧǿ��ΪB����ǿ�ų�����ֱ��ֽ�����⣮������ab������Ϊm���뵼��Ӵ����ã�����Ħ�����Ӿ�ֹ�ͷź�ab����ˮƽ���»�������