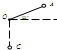题目内容
长为L的轻悬线，一端固定于O点，另一端栓一个质量为m的小球．在O点的正下方L/2处钉有一颗钉子P，把悬线沿水平方向拉直，如图所示，无初速度释放，当悬线碰到钉子后的瞬时（线没有断），则（ ）分析：把悬线沿水平方向拉直后无初速度释放，当悬线碰到钉子的前后瞬间，线速度大小不变，半径减小，根据v=rω、a=
判断角速度、向心加速度大小的变化，根据牛顿第二定律判断悬线拉力的变化．
| v2 |
| r |
解答：解：A、B把悬线沿水平方向拉直后无初速度释放，当悬线碰到钉子的前后瞬间，线速度大小不变，半径变小，根据v=rω，则角速度增大．故AB错误．
C、当悬线碰到钉子后，半径是原来的一半，线速度大小不变，则由a=
分析可知，向心加速度突然增加为碰钉前的2倍．故C正确．
D、根据牛顿第二定律得：
悬线碰到钉子前瞬间：T1-mg=m
得，T1=mg+m
悬线碰到钉子后瞬间：T2-mg=m
得，T2=mg+2m
由数学知识知：T2＜2T1．故D错误．
故选C．
C、当悬线碰到钉子后，半径是原来的一半，线速度大小不变，则由a=
| v2 |
| r |
D、根据牛顿第二定律得：
悬线碰到钉子前瞬间：T1-mg=m
| v2 |
| L |
| v2 |
| L |
悬线碰到钉子后瞬间：T2-mg=m
| v2 | ||
|
| v2 |
| L |
由数学知识知：T2＜2T1．故D错误．
故选C．
点评：解决本题的关键要掌握线速度、角速度、向心加速度之间的关系，以及知道在本题中悬线碰到钉子的前后瞬间，线速度大小不变．
练习册系列答案
相关题目
如图所示，一根长为L的轻质细线，一端固定于O点，另一端拴有一质量为m的小球，可在竖直的平面内绕O点摆动，现拉紧细线使小球位于与O点在同一竖直面内的A位置，细线与水平方向成30°角，从静止释放该小球，当小球运动至悬点正下方C位置时的速度是（ ）
