Question

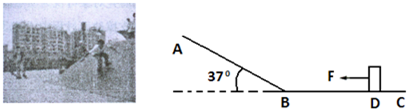
滑板运动是以滑行为特色，崇尚自由的一种运动方式，给滑者带来成功和创造的喜悦．若滑道简化为倾角为θ=37⁰的斜面．AB及水平面BC，斜面与水平面平滑连接．运动员简化为质量m=2kg的木块，置于水平面上的D点．DB间距d=7m，木块与斜面、水平面间的动摩擦因数皆为?=0.2，将一水平向左的恒力F=8N作用在该物体上，t=2s后撤去该力，不考虑物体经过B点时的碰撞损失，重力加速度取g=10m/s²，斜面足够长．求撤去拉力F后，经过多长时间物体经过B点？

Answer 1

设在F的作用下物体运动的加速度为a₁，则有
   F-μmg=ma，得a₁=2m/s²．
作用t₁=2s后物体的速度为v₁=a₁t₁=4m/s，位移为s₁=

1

2

a1

t

21

=4m
设撤去F后，物体加速度大小为a₂，则a₂=

μmg

m

=2m/s²．
设第一次到达B点所用时间为t₂，则
   d-s₁=v₁t₂-

1

2

a2

t

22

解得，t₂=1s
此时物体的速度为v₂=v₁-a₂t₂=2m/s
物体从B点上滑的过程中，加速度大小为a₃=

mgsin37°+μmgcos37°

m

=7.6m/s2
上滑时间为t₃=

v2

a3

=

2

7.6

s≈0.26s
设物体由斜面最高点重回B点时经过时间为t₄，加速度为a₄，
则  a₄=

mgsin37°-μmgcos37°

m

=4.4m/s²
由s₄=s₃=

1

2

a4

t

24

，得t₄≈0.35s
所以撤去拉力后，物体第二次经过B点的时间为t₂+t₃+t₄=1.61s．
答：物体第一次到达B点所用时间为1s，第二次经过B点的时间为1.61s．