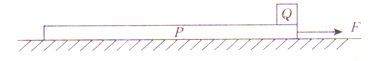题目内容
【题目】类比法、等效法等都是研究和学习物理过程中常用的重要方法：
(1)简谐运动是机械振动中最简单的一种理想化的运动模型。它具有如下特点：①简谐运动的物体受到的回复力，大小与物体偏离平衡位置的位移 x 成正比，方向与 x 方向相反；②简谐运动具有周期性。
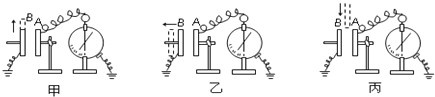
通过研究发现：如图甲，摆长为 L、摆球质量为 m 的单摆，在重力场中做小角度摆动时可以看作简谐振动，其周期为T = 2π
，g 为当地重力加速度；
现将该单摆的摆球带上正电，电量为+q。分别置于竖直向下的匀强电场E（图乙）、和垂直于纸面向里的匀强磁场 B（图丙）中，并均做小角度的简谐运动。已知细线是绝缘的，类比重力场中的单摆周期公式，分析求出该单摆在乙、丙两图中振动的周期。
(2)物理中存在“通量”这个物理量，“通量”的定义要用到高等数学知识。在高中阶段，对“通量”的定义采用的是简单化处理方法并辅以形象化物理模型进行理解。
①“磁通量”就是一种常见的“通量”。在高中阶段我们是这样来定义“磁通量”的：设在磁感应强度为B 的匀强磁场中，有一个与磁场方向垂直、面积为 S 的平面，我们把 B 与 S 的乘积叫做穿过这个面积的磁通量（图1），简称磁通，用字母 Φ 表示，则 Φ=BS。
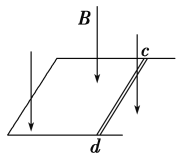
如图2所示，空间存在水平向右的匀强磁场，磁感应强度大小为 B。一个面积为S 矩形线圈与竖直面间的夹角为θ，试求穿过该矩形线圈的磁通量 Φ。
② “电通量”也是一种常见“通量”。在定义“电通量”时只需要把“磁通量”中的磁感应强度 B 替换为电场强度 E即可。已知静电力常量为 k，请同学们充分运用类比的方法解决以下问题：
a.如图 3，空间存在正点电荷Q ，以点电荷为球心作半径为 R 的球面。试求通过该球面的电通量 ΦE1；
b.上述情况映射的是静电场中“高斯定理”，“高斯定理”可以从库仑定律出发得到严格证明。“高斯定理”可表述为：通过静电场中任一闭合曲面的电通量等于闭合曲面内所含电荷量 Q 与 4πk 的乘积，即 ΦE=4πkQ；试根据“高斯定理”证明：一个半径为R的均匀带电球体（或球壳）在外部产生的电场，与一个位于球心的、电荷量相等的点电荷产生的电场相同，球外各点的电场强度也是 
=k
（r
），式中 r 是球心到该点的距离，为整个球体所带的电荷量。
【答案】（1）
，
；（2）a.
，b.证明见解析
【解析】
(1)图乙中，摆球受到重力G、电场力F电和摆线拉力T，与重力场中的单摆类比，
等效的“重力”
，
带入单摆周期公式得
图丙中，摆球受到重力G、洛伦兹力F洛和摆线拉力T，与重力场中的单摆类比，洛伦兹力始终沿摆线方向，不产生回复力的效果
单摆周期与重力场中相同
(2)①当面积为
的矩形线圈与竖直面间的夹角为
时，线圈在磁场垂直方投影面积为
，磁通量
(2)a.根据点电荷的场强公式，求得球面上各处的电场强度大小为
由于球面上各处电场强度方向都与球面垂直，故通过球面的电通量为
b.证明：过距离球心距离
的点作一球面，根据对称性可知该球面上各点场强大小相等，方向处处球面垂直。设该点的电场强度为
，通过该球面的电通量为
，则有
由高斯定理知
所以有
化简得
这就是球心处的点电荷
在处产生的场强，证明完毕。
