题目内容
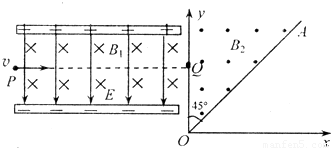
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直于纸面向里,电场强度E=2.0×105V/m,PQ为板间中线,紧靠平行板右侧边缘xoy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电荷量q=8.0×10-19C的正粒子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区域,粒子通过x轴时的速度方向与x轴正方向夹角为45°.不考虑重力的影响.求:(1)粒子运动的速度v是多大?
(2)粒子的质量m是多大?
【答案】分析:(1)带电粒子在复合场中受电场力和洛伦兹力平衡,根据平衡条件列式得到速度;
(2)粒子离开复合场后进入又一个匀强磁场后做匀速圆周运动,根据几何关系先确定圆心和半径,再根据洛伦兹力提供向心力列式得到粒子的质量.
解答:解:(1)粒子沿中线PQ做直线运动,则qB1v=qE
v=5×105m/s
即粒子运动的速度v是5×105m/s.
(2)粒子在AOy区域内做匀速圆周运动,设半径为r,则
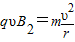
粒子穿过AO后做匀速直线运动,由于粒子通过x轴时的速度方向与x轴正方向夹角为45°
所以,粒子离开AO时与AO垂直,
所以O是做匀速圆周运动的圆心,
则r=OQ=0.2m
解得m=8×10-26kg
故粒子的质量m是8×10-26kg.
点评:本题中粒子先通过速度选择器,然后在匀强磁场中做匀速圆周运动,根据洛伦兹力提供向心力列式求解;带电粒子在匀速磁场中做匀速圆周运动问题通常要先确定圆心,得到半径,最后根据洛伦兹力提供向心力列式.
(2)粒子离开复合场后进入又一个匀强磁场后做匀速圆周运动,根据几何关系先确定圆心和半径,再根据洛伦兹力提供向心力列式得到粒子的质量.
解答:解:(1)粒子沿中线PQ做直线运动,则qB1v=qE
v=5×105m/s
即粒子运动的速度v是5×105m/s.
(2)粒子在AOy区域内做匀速圆周运动,设半径为r,则
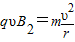
粒子穿过AO后做匀速直线运动,由于粒子通过x轴时的速度方向与x轴正方向夹角为45°
所以,粒子离开AO时与AO垂直,
所以O是做匀速圆周运动的圆心,
则r=OQ=0.2m
解得m=8×10-26kg
故粒子的质量m是8×10-26kg.
点评:本题中粒子先通过速度选择器,然后在匀强磁场中做匀速圆周运动,根据洛伦兹力提供向心力列式求解;带电粒子在匀速磁场中做匀速圆周运动问题通常要先确定圆心,得到半径,最后根据洛伦兹力提供向心力列式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直于纸面向里,电场强度E=2.0×105V/m,PQ为板间中线,紧靠平行板右侧边缘xoy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电荷量q=8.0×10-19C的正粒子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区域,粒子通过x轴时的速度方向与x轴正方向夹角为45°.不考虑重力的影响.求:
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直于纸面向里,电场强度E=2.0×105V/m,PQ为板间中线,紧靠平行板右侧边缘xoy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电荷量q=8.0×10-19C的正粒子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区域,粒子通过x轴时的速度方向与x轴正方向夹角为45°.不考虑重力的影响.求:
 如图所示的平行板器件中.电场强度E和磁感应强度B相互垂直,具有不同水平速度的带电粒子从P孔射入后发生偏转的情况不同.利用这种装置能把具有某一特定速度的粒子选择出来,所以叫做速度选择器.若正离子(不计重力)以水平速度v=
如图所示的平行板器件中.电场强度E和磁感应强度B相互垂直,具有不同水平速度的带电粒子从P孔射入后发生偏转的情况不同.利用这种装置能把具有某一特定速度的粒子选择出来,所以叫做速度选择器.若正离子(不计重力)以水平速度v= 如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20T,方向垂直纸面向里,电场强度E1=1.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xoy坐标系的第一象限内,有一边界AO,与y轴的夹角∠AOy=45°,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度 B2=0.25T,边界线的下方有竖直向上的匀强电场,电场强度E2=5.0×105V/m,一束带电量q=8.0×10-19C、质量m=8.0×10-26kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.4m)的Q点垂直y轴射入磁场区,多次穿越边界限OA.求:
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20T,方向垂直纸面向里,电场强度E1=1.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xoy坐标系的第一象限内,有一边界AO,与y轴的夹角∠AOy=45°,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度 B2=0.25T,边界线的下方有竖直向上的匀强电场,电场强度E2=5.0×105V/m,一束带电量q=8.0×10-19C、质量m=8.0×10-26kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.4m)的Q点垂直y轴射入磁场区,多次穿越边界限OA.求: (2011?浙江模拟)如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域,磁感应强度B2=0.25T.一束带电量q=8.0×10-19C,质量m=8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°.则:
(2011?浙江模拟)如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域,磁感应强度B2=0.25T.一束带电量q=8.0×10-19C,质量m=8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°.则: