题目内容
13. 如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?
如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?
分析 本题可以分为两个过程来求解,首先根据AB系统的机械能守恒,可以求得A球上升h时的速度的大小,之后,B球落地,A球的机械能守恒,从而可以求得A球上升的高度的大小.
解答 解:据题意分析可知,AB一起运动,当B着地后,A向上做匀减速直线运动.
B着地,由动能定理得:
mBgh-mAgh=$\frac{1}{2}$(mA+mB)v2
A继续上升,由机械能守恒定律可得:
mAgh′=$\frac{1}{2}$mAv2
依题意:h+h′=0.9
联合三式,解得B物体原来离地面的高度:h=0.6m
答:B物体原来离地面的高度h等于 0.6m.
点评 在A球上升的全过程中,A球的机械能是不守恒的,所以在本题中要分过程来求解,第一个过程系统的机械能守恒,在第二个过程中只有a球的机械能守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列现象中属于不浸润现象的是( )
| A. | 使用钢笔难以在油纸上写出字迹 | |
| B. | 洒在玻璃板上的水滴会迅速向四周扩展 | |
| C. | 少量的水洒在蜡纸上,成球形水珠 | |
| D. | 少量的油在汤里形成小油珠 | |
| E. | 从房檐低落的水成下大上小的水滴 | |
| F. | 沾了油的抹布,不能把带水的桌面擦干 | |
| G. | 内径很小的玻璃管竖直插在水银槽内,细管内的水银面比外面槽里的水银面低 |
18.我们经常在电视中看到男、女花样滑冰运动员手拉手在冰面上旋转并表演各种优美的动作.现有甲、乙两名花样滑冰运动员,M甲=80kg,M乙=40kg,他们面对面拉着弹簧测力计各自以他们连线上某一点为圆心做匀速圆周运动,若两人相距0.9m,弹簧测力计的示数为600N,则( )
| A. | 两人的线速度相同,为0.4 m/s | |
| B. | 两人的角速度相同,为5.0 rad/s | |
| C. | 两人的运动半径相同,都是0.45 m | |
| D. | 两人的运动半径不同,甲的半径是0.3m、乙的半径是0.6 m |
5. 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )| A. | $\frac{1}{2}$mgR | B. | mgR | C. | 2mgR | D. | $\frac{5}{2}$mgR |
2.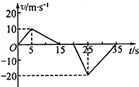 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )| A. | 在0~15s内,观光电梯上升的高度为25m | |
| B. | 在5~15s内,电梯内的同学处于超重状态 | |
| C. | 在20~25s与25~35s内,观光电梯的平均速度大小均为10m/s | |
| D. | 在25~35s内,观光电梯在减速上升,该同学的加速度大小2m/s2 |
3.三个电流表A1、A2、A3分别与电容器、电阻器、电感器串接在一起,接到一电压最大值不变但频率可变的交流电源上,当使交变电流的频率增加时,下列说法正确的是( )
| A. | 三个电流表示数不变 | B. | 三个表的示数都增加 | ||
| C. | A2表的示数变小 | D. | A3表的示数变小 |
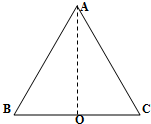 如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少?
如图所示为一等边三角形的某种透明介质ABC,边长为L,折射率为$\frac{5}{3}$,底部中点O处有一点光源,试问能够从AB边射出光线的长度是多少? 如图所示,有一个边界为正三角形的匀强磁场区域,边长为a,磁感应强度方向垂直纸面向里,一个矩形导体框的长为a、宽为.若导体框平行于纸面沿着磁场区域的轴线匀速穿越磁场区域,取导体框中感应电流的逆时针方向为正方向,以导体框刚进入磁场时为t=0时刻.则在穿过磁场的过程中,导体框中的感应电流随时间变化的图象是图中的( )
如图所示,有一个边界为正三角形的匀强磁场区域,边长为a,磁感应强度方向垂直纸面向里,一个矩形导体框的长为a、宽为.若导体框平行于纸面沿着磁场区域的轴线匀速穿越磁场区域,取导体框中感应电流的逆时针方向为正方向,以导体框刚进入磁场时为t=0时刻.则在穿过磁场的过程中,导体框中的感应电流随时间变化的图象是图中的( )


