题目内容
 如图所示,在倾角θ的粗糙斜面上放一物体,质量为m,现在用与斜面底边平行的力F推物体,物体恰能在斜面上斜向下匀速直线运动,物体与斜面之间的动摩擦因数为?,则F与m关系为( )
如图所示,在倾角θ的粗糙斜面上放一物体,质量为m,现在用与斜面底边平行的力F推物体,物体恰能在斜面上斜向下匀速直线运动,物体与斜面之间的动摩擦因数为?,则F与m关系为( )分析:物体在斜面上做匀速直线运动,受力平衡,分析受力情况,将重力分解,作出物体在平行于斜面上的受力示意图.根据平衡条件求出物体所受的滑动摩擦力和支持力,再求解即可.
解答: 解:将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则
解:将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则
支持力 FN=mgcosθ.
在斜面内,物体所受的推力F、摩擦力Ff与重力的平行斜面的分力mgsinθ平衡,如图所示.
由物体的平衡条件得滑动摩擦力为:Ff=
,则得:F<Ff
物体与斜面间的摩擦力 Ff=μFN=μmgcosθ.
所以有:F<μmgcosθ.
故选:C
 解:将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则
解:将物体的重力分解为垂直于斜面和平行于斜面两个方向的分力,在垂直于斜面的方向上,物体受到的支持力与重力垂直斜面的分力平衡.则支持力 FN=mgcosθ.
在斜面内,物体所受的推力F、摩擦力Ff与重力的平行斜面的分力mgsinθ平衡,如图所示.
由物体的平衡条件得滑动摩擦力为:Ff=
| (mgsinθ)2+F2 |
物体与斜面间的摩擦力 Ff=μFN=μmgcosθ.
所以有:F<μmgcosθ.
故选:C
点评:本题物体受力分布在立体空间,分成垂直于斜面和平行于斜面两平面内研究,任何一个平面内物体的合力都为零.

练习册系列答案
相关题目
 如图所示,在倾角为θ的光滑斜面上,重为G的物体受到水平推力F的作用,物体静止不动,则物体对斜面的压力大小为( )
如图所示,在倾角为θ的光滑斜面上,重为G的物体受到水平推力F的作用,物体静止不动,则物体对斜面的压力大小为( )A、
| ||
B、
| ||
| C、Gcosθ+Fsinθ | ||
| D、Gcosθ+Fcosθ |
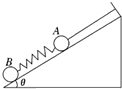 如图所示,在倾角为θ的光滑斜面上有A、B两个小球,A、B球的质量相等,弹簧的质量不计,系统静止时,弹簧与细线均平行于斜面,在细线被烧断的瞬间,下列说法正确的是( )
如图所示,在倾角为θ的光滑斜面上有A、B两个小球,A、B球的质量相等,弹簧的质量不计,系统静止时,弹簧与细线均平行于斜面,在细线被烧断的瞬间,下列说法正确的是( )| A、两个小球的瞬时加速度均沿斜面向下,大小均为gsinθ | B、B球的受力情况未变,瞬时加速度为零 | C、A球的瞬时加速度沿斜面向下,大小为2gsinθ | D、弹簧有收缩的趋势,B球的瞬时加速度向上,A球的瞬时加速度向下 |
 如图所示,在倾角为θ的粗糙程度相同的斜面上,两相同的木块A、B靠在一起沿斜面下滑,在两木块下滑过程中,关于木块A受力情况的说法正确的是( )
如图所示,在倾角为θ的粗糙程度相同的斜面上,两相同的木块A、B靠在一起沿斜面下滑,在两木块下滑过程中,关于木块A受力情况的说法正确的是( )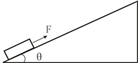 如图所示,在倾角θ=370的足够长的固定斜面底端有一质量m=1.0kg的物体,物体与斜面间动摩擦因数μ=0.25,现用平行斜面向上拉力F=10N将物体由静止沿斜面向上拉动,经时间t=4.0s撤去F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,在倾角θ=370的足够长的固定斜面底端有一质量m=1.0kg的物体,物体与斜面间动摩擦因数μ=0.25,现用平行斜面向上拉力F=10N将物体由静止沿斜面向上拉动,经时间t=4.0s撤去F,(sin37°=0.6,cos37°=0.8,g=10m/s2)求: 如图所示,在倾角θ=37°的固定斜面底端,放着一个质量为1Kg的物体,现对物体施加平行于斜面向上的恒力F=20N,作用时间t1=1s时撤去拉力F,若物体与斜面间的动摩擦因数为μ=0.5,斜面足够长,取g=10m/s2,sin37°=0.6,cos37°=0.8.试求:
如图所示,在倾角θ=37°的固定斜面底端,放着一个质量为1Kg的物体,现对物体施加平行于斜面向上的恒力F=20N,作用时间t1=1s时撤去拉力F,若物体与斜面间的动摩擦因数为μ=0.5,斜面足够长,取g=10m/s2,sin37°=0.6,cos37°=0.8.试求: