题目内容
如图甲所示，A、B是一列简谐横波中的两点，某时刻，A正处于正向最大位移处，另一点B恰好通过平衡位置向-y方向振动．已知A、B的横坐标分别为XA=0，XB=70m，并且波长λ符合不等式：20＜λ＜80m，求波长λ．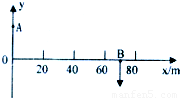
【答案】分析：依题意，A正处于正向最大位移处，另一点B恰好通过平衡位置向-y方向振动，波的传播方向未知，分别研究波向右和向左传播时波长与AB间距离的关系，求出波长的通项式，再结合条件20＜λ＜80m，求出波长值．
解答：解：若波向右传播，则有
△x=（n+
）λ1，n=0，1，2，…
得到波长λ1=
=
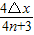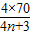m=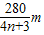
结合条件20m＜λ＜80m，即2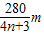0m＜
＜80m，
解得
＜n＜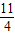
，由于n是整数，则n取1，2
得到波长为：40m，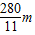
若波向左传播，则有
△x=（n+
）λ2，n=0，1，2，…
同理得到波长为：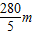
，
，
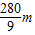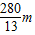
答：当波向右传播时，波长为40m，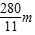
；若波向左传播时，波长为：
，
，
．
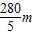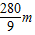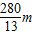点评：本题是常见的题型，在波的传播方向未知时，要考虑波的双向性，不能漏解．常常通过画波形研究，根据波形的平衡法距离与波长的关系．
解答：解：若波向右传播，则有
△x=（n+
）λ1，n=0，1，2，…得到波长λ1=
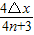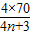=m=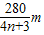结合条件20m＜λ＜80m，即2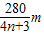0m＜
＜80m，解得
＜n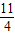＜，由于n是整数，则n取1，2得到波长为：40m，
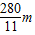
若波向左传播，则有
△x=（n+
）λ2，n=0，1，2，…同理得到波长为：
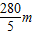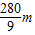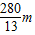
，，答：当波向右传播时，波长为40m，
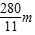；若波向左传播时，波长为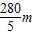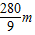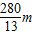：，，．点评：本题是常见的题型，在波的传播方向未知时，要考虑波的双向性，不能漏解．常常通过画波形研究，根据波形的平衡法距离与波长的关系．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
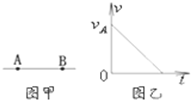如图甲所示，A、B是一条电场线上的两点，当一个电子以某一初速度只在电场力作用下沿AB由A点运动到B点，其速度-时间图象如图乙所示，电子到达B点时速度恰为零．下列判断正确的是（ ）
如图甲所示，A、B 是一对平行金属板． A 板的电势φA=0，B 板的电势φB随时间的变化规律为如图乙所示，现有一电子从 A 板上的小孔进入板间的电场区内．电子的初速度和重力的影响均可忽略，则（ ）
如图甲所示，A、B是叠放在光滑水平面上的两物块，两物块质量均为m，水平力F作用在物块B上，A、B一起从静止开始做直线运动（无相对滑动），F随时间t变化关系如图乙所示．下列说法正确的是（ ）
（2013?马鞍山三模）Ⅰ在《验证力的平行四边形定则》的实验中，某同学的实验情况如图甲所示，其中A为固定橡皮筋的图钉，O为橡皮条与细绳的结点，OB和OC为细绳．图乙是在白纸上根据实验结果画出的图，则：