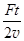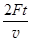题目内容
1932年，劳伦斯和利文斯设计出了回旋加速器．回旋加速器的工作原理如图所示，置于真空中的两个D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计．磁感应强度为B的匀强磁场与盒面垂直. 设两D形盒之间所加的交流电压为U，被加速的粒子质量为m、电量为q,粒子从D形盒一侧开始被加速（初动能可以忽略），经若干次加速后粒子从D形盒边缘射出．
求：（1）粒子从静止开始第1次经过两D形盒间狭缝加速后的速度大小
（2）粒子第一次进入D型盒磁场中做圆周运动的轨道半径
（3）粒子至少经过多少次加速才能从回旋加速器D形盒射出
求：（1）粒子从静止开始第1次经过两D形盒间狭缝加速后的速度大小
（2）粒子第一次进入D型盒磁场中做圆周运动的轨道半径
（3）粒子至少经过多少次加速才能从回旋加速器D形盒射出
（1）
（2）
（3）
（2）（3）试题分析：（1）(5分)粒子在电场中被加速由动能定理
…………4分 得:
…………………………………………………………1分（2）(5分)带电粒子在磁场中做圆周运动，洛仑兹力提供向心力，
由牛顿第二定律得：
………………………………………3分解得：
……………………………………………1分代入数据得：
…………………………………1分（3）(6分)若粒子射出，则粒子做圆周运动的轨道半径为R,设此时速度为
由牛顿第二定律知
，解得此时粒子的速度为
……2分此时粒子的动能为
代入数据得
………………2分粒子每经过一次加速动能增加qU，设经过n次加速粒子射出，则
代入数据，解得： ………………………………2分
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
