题目内容
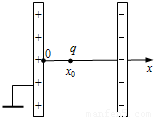 如图所示,平行板电容器两极板间有场强为E的匀强电场,且带正电的极板接地.一质量为m,电荷量为+q的带电粒子(不计重力)从x轴上坐标为x处静止释放.
如图所示,平行板电容器两极板间有场强为E的匀强电场,且带正电的极板接地.一质量为m,电荷量为+q的带电粒子(不计重力)从x轴上坐标为x处静止释放.(1)求该粒子在x处电势能Epx0.
(2)试从牛顿第二定律出发,证明该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
【答案】分析:电势能的大小等于从该点运动电荷到无穷远处时电场力做的功.代入公式即可.
解答:解:(1)W电=qEx0…①
W电=-(Epx0-0)…②
联立①②得Epx0=-qEx0
(2)解法一
在带电粒子的运动方向上任取一点,设坐标为 x
由牛顿第二定律可得
qE=ma…④
由运动学公式得
V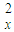 =2a(x-x)…⑤
=2a(x-x)…⑤
联立④⑤进而求得:
Ekx= mv
mv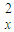 =qE(x-x)
=qE(x-x)
E=Ekx+Epx=-qEx=Ex0
(2)解法二
在 x轴上任取两点 x1、x2,速度答:分别为 v1、v2
F=qE=ma
v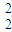 -v
-v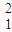 =2a(x2-x1)
=2a(x2-x1)
联立得:
 mv
mv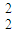 -
- m v
m v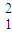 =qE(x2-x1)
=qE(x2-x1)
 m v
m v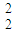 +(-qEx2)=
+(-qEx2)= m v
m v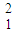 +(-qEx1)
+(-qEx1)
Ek2+EP2=Ek1+Ep1
答:(1)该粒子在x处电势能-qEx0
(2)该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
点评:该题考查电势能的特性,电势能的大小等于从该点运动电荷到无穷远处时电场力做的功.属于基础题目.
解答:解:(1)W电=qEx0…①
W电=-(Epx0-0)…②
联立①②得Epx0=-qEx0
(2)解法一
在带电粒子的运动方向上任取一点,设坐标为 x
由牛顿第二定律可得
qE=ma…④
由运动学公式得
V
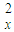 =2a(x-x)…⑤
=2a(x-x)…⑤联立④⑤进而求得:
Ekx=
 mv
mv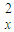 =qE(x-x)
=qE(x-x)E=Ekx+Epx=-qEx=Ex0
(2)解法二
在 x轴上任取两点 x1、x2,速度答:分别为 v1、v2
F=qE=ma
v
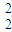 -v
-v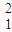 =2a(x2-x1)
=2a(x2-x1)联立得:
 mv
mv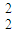 -
- m v
m v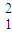 =qE(x2-x1)
=qE(x2-x1) m v
m v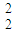 +(-qEx2)=
+(-qEx2)= m v
m v +(-qEx1)
+(-qEx1)Ek2+EP2=Ek1+Ep1
答:(1)该粒子在x处电势能-qEx0
(2)该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
点评:该题考查电势能的特性,电势能的大小等于从该点运动电荷到无穷远处时电场力做的功.属于基础题目.

练习册系列答案
相关题目
 如图所示,平行板电容器中间充有电介质,现要使此电容器的电容增大,下列措施中正确的是( )
如图所示,平行板电容器中间充有电介质,现要使此电容器的电容增大,下列措施中正确的是( )| A、将电介质从电容器中抽出 | B、增大两极板间的距离 | C、减小两极板间的距离 | D、减小极板间的正对面积 |
 如图所示,平行板电容器与直流电源连接,下极板接地.一带电油滴位于电容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( )
如图所示,平行板电容器与直流电源连接,下极板接地.一带电油滴位于电容器中的P点且恰好处于平衡状态.现将平行板电容器的上极板竖直向上移动一小段距离( ) (2007?淮安模拟)如图所示,平行板电容器与恒定电源相连,负极板接地,在两板间有一正电荷(电荷量很少且不变)固定在P点,以U表示电容两极板间的电压,E表示两极板间的场强,Ep表示正电荷在P点的电势能,若保持负极板不动,而将正极板向上移至某位置,则
(2007?淮安模拟)如图所示,平行板电容器与恒定电源相连,负极板接地,在两板间有一正电荷(电荷量很少且不变)固定在P点,以U表示电容两极板间的电压,E表示两极板间的场强,Ep表示正电荷在P点的电势能,若保持负极板不动,而将正极板向上移至某位置,则 如图所示,平行板电容器的两个极板A、B分别接在电压为60V的恒压电源上,两极板间距为3cm,电容器带电荷量为6×10-8C,A极板接地(电势为零).求:
如图所示,平行板电容器的两个极板A、B分别接在电压为60V的恒压电源上,两极板间距为3cm,电容器带电荷量为6×10-8C,A极板接地(电势为零).求: 如图所示,平行板电容器通过一滑动变阻器R与直流电源连接,G为一零刻度在表盘中央的电流计,闭合开关S后,下列说法中正确的是( )
如图所示,平行板电容器通过一滑动变阻器R与直流电源连接,G为一零刻度在表盘中央的电流计,闭合开关S后,下列说法中正确的是( )