题目内容
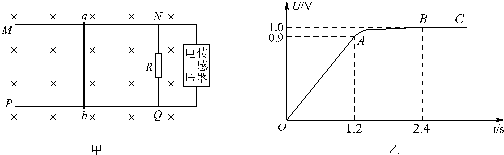
如图甲所示,MN、PQ为间距L=0.5m足够长的平行粗糙导轨,NQ⊥MN,导轨的电阻均不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行s=2m至cd处时达到稳定速度,已知在此过程中金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(sin37°=0.6,cos37°=0.8,g=10m/s2).求:(1)金属棒刚释放时的加速度a以及金属棒与导轨间的动摩擦因数μ
(2)金属棒滑行至cd处的过程中,金属棒上产生的热量Q
(3)金属棒由静止释放到达到稳定速度的过程中,通过金属棒的电荷量q
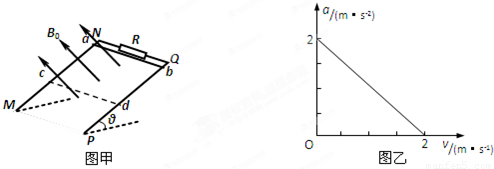
【答案】分析:(1)由a-v图象读出v=0时,a=2m/s2.根据牛顿第二定律列方程,求解μ.
(2)由FA=BIL、E=BLv、I=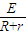 推导出安培力的表达式,属棒滑行至cd处时,金属棒做匀速运动,由平衡条件求出导体棒的电阻r.当a=0时,金属棒做匀速运动,由图读出a=0时,v=2m/s,由能量守恒定律求解金属棒滑行至cd处的过程中,回路中产生的总热量Q,由串联关系知,金属棒上产生的热量Qr=
推导出安培力的表达式,属棒滑行至cd处时,金属棒做匀速运动,由平衡条件求出导体棒的电阻r.当a=0时,金属棒做匀速运动,由图读出a=0时,v=2m/s,由能量守恒定律求解金属棒滑行至cd处的过程中,回路中产生的总热量Q,由串联关系知,金属棒上产生的热量Qr=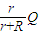 .
.
(3)根据法拉第电磁感应定律、欧姆定律、q=I△t联立解出电量.
解答:解:(1)由图知,当v=0时,a=2m/s2.
根据牛顿第二定律得:
mgsinθ-μmgcosθ=ma
解得μ=0.5
(2)由FA=BIL、E=BLv、I=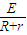 得
得
安培力FA=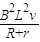
由图知,a=0时,v=2m/s,即金属棒匀速运动时速度为2m/s.则由平衡条件得
mgsinθ=FA+μmgcosθ
联立解得,r=1Ω
金属棒滑行s=2m至cd处的过程中,根据能量守恒定律得
mgs?sin37°-μmhscos37°-Q=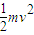
解得,电路中产生的总热量为Q=0.1J
根据串联关系,由焦耳定律得
金属棒上产生的热量Qr=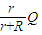 =0.02J.
=0.02J.
(3)由图象可知:v=2m/s.当金属棒达到稳定速度时,有
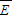 =
=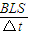
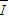 =
=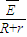
q=
解得,电量q=0.4C.
答:
(1)金属棒刚释放时的加速度a是2m/s2.金属棒与导轨间的动摩擦因数μ是0.5.
(2)金属棒滑行至cd处的过程中,金属棒上产生的热量Q是0.02J.
(3)金属棒由静止释放到达到稳定速度的过程中,通过金属棒的电荷量q是0.4C.
点评:本题通过图象反映金属棒的运动过程,由图读出加速度和速度,根据金属棒的状态,由牛顿第二定律和平衡条件、能量守恒定律综合研究.
(2)由FA=BIL、E=BLv、I=
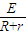 推导出安培力的表达式,属棒滑行至cd处时,金属棒做匀速运动,由平衡条件求出导体棒的电阻r.当a=0时,金属棒做匀速运动,由图读出a=0时,v=2m/s,由能量守恒定律求解金属棒滑行至cd处的过程中,回路中产生的总热量Q,由串联关系知,金属棒上产生的热量Qr=
推导出安培力的表达式,属棒滑行至cd处时,金属棒做匀速运动,由平衡条件求出导体棒的电阻r.当a=0时,金属棒做匀速运动,由图读出a=0时,v=2m/s,由能量守恒定律求解金属棒滑行至cd处的过程中,回路中产生的总热量Q,由串联关系知,金属棒上产生的热量Qr=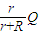 .
.(3)根据法拉第电磁感应定律、欧姆定律、q=I△t联立解出电量.
解答:解:(1)由图知,当v=0时,a=2m/s2.
根据牛顿第二定律得:
mgsinθ-μmgcosθ=ma
解得μ=0.5
(2)由FA=BIL、E=BLv、I=
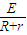 得
得安培力FA=
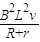
由图知,a=0时,v=2m/s,即金属棒匀速运动时速度为2m/s.则由平衡条件得
mgsinθ=FA+μmgcosθ
联立解得,r=1Ω
金属棒滑行s=2m至cd处的过程中,根据能量守恒定律得
mgs?sin37°-μmhscos37°-Q=
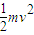
解得,电路中产生的总热量为Q=0.1J
根据串联关系,由焦耳定律得
金属棒上产生的热量Qr=
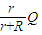 =0.02J.
=0.02J.(3)由图象可知:v=2m/s.当金属棒达到稳定速度时,有
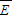 =
=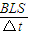
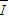 =
=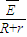
q=

解得,电量q=0.4C.
答:
(1)金属棒刚释放时的加速度a是2m/s2.金属棒与导轨间的动摩擦因数μ是0.5.
(2)金属棒滑行至cd处的过程中,金属棒上产生的热量Q是0.02J.
(3)金属棒由静止释放到达到稳定速度的过程中,通过金属棒的电荷量q是0.4C.
点评:本题通过图象反映金属棒的运动过程,由图读出加速度和速度,根据金属棒的状态,由牛顿第二定律和平衡条件、能量守恒定律综合研究.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图甲所示,MN为一原来不带电的导体棒,q为一带电量恒定的点电荷,当达到静电平衡后,导体棒上的感应电荷在棒内P点处产生的场强大小为E1,p点的电势为U1.现用一导线将导体棒的N端接地,其它条件不变,如图乙所示,待静电平衡后,导体棒上的感应电荷在棒内P点处产生的场强为E2,P点的电势为U2,则( )
如图甲所示,MN为一原来不带电的导体棒,q为一带电量恒定的点电荷,当达到静电平衡后,导体棒上的感应电荷在棒内P点处产生的场强大小为E1,p点的电势为U1.现用一导线将导体棒的N端接地,其它条件不变,如图乙所示,待静电平衡后,导体棒上的感应电荷在棒内P点处产生的场强为E2,P点的电势为U2,则( ) 如图甲所示,MN为很大的薄金属板(可理解为无限大),金属板原来不带电.在金属板的右侧,距金属板距离为d的位置上放入一个带正电、电荷量为q的点电荷,由于静电感应产生了如图甲所示的电场分布.P是点电荷右侧,与点电荷之间的距离也为d的一个点,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别求出了P点的电场强度大小,一共有以下四个不同的答案(k为静电力常量),其中正确的是( )
如图甲所示,MN为很大的薄金属板(可理解为无限大),金属板原来不带电.在金属板的右侧,距金属板距离为d的位置上放入一个带正电、电荷量为q的点电荷,由于静电感应产生了如图甲所示的电场分布.P是点电荷右侧,与点电荷之间的距离也为d的一个点,几位同学想求出P点的电场强度大小,但发现问题很难.几位同学经过仔细研究,从图乙所示的电场得到了一些启示,经过查阅资料他们知道:图甲所示的电场分布与图乙中虚线右侧的电场分布是一样的.图乙中两异号点电荷电荷量的大小均为q,它们之间的距离为2d,虚线是两点电荷连线的中垂线.由此他们分别求出了P点的电场强度大小,一共有以下四个不同的答案(k为静电力常量),其中正确的是( )