题目内容
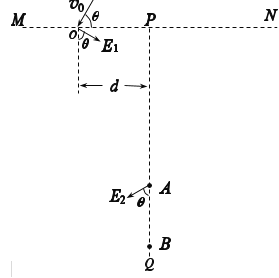
【题目】某实验小组利用如图所示装置“探究加速度与物体受力的关系”，已知小车的质量为M，单个钩码的质量为m，打点计时器所接的交流电源的频率为50 Hz，动滑轮质量不计，实验步骤如下：
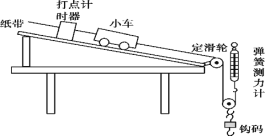
①按图所示安装好实验装置，其中与定滑轮及弹簧测力计相连的细线竖直；
②调节长木板的倾角，轻推小车后，使小车能沿长木板向下匀速运动；
③挂上钩码，接通电源后，再放开小车，打出一条纸带，由纸带求出小车的加速度；
④改变钩码的数量，重复步骤③，求得小车在不同合力作用下的加速度。
根据上述实验过程，回答以下问题：
(1)对于上述实验，下列说法正确的是__________ (填选项前的字母)。
A．钩码的质量应远小于小车的质量 B．实验过程中钩码处于超重状态
C．与小车相连的细线与长木板一定要平行 D．弹簧测力计的读数应为钩码重力的一半
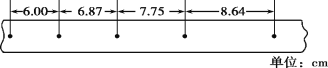
(2)实验中打出的一条纸带如图所示，图中两邻两计数点间还有4个点未画出，由该纸带可求得小车的加速度a=__________m/s2(结果保留两位有效数字)。
(3)若交流电的实际频率大于50 Hz，则上述(2)中加速度a计算结果与实际值相比__________(选填“偏大”、“偏小”、“不变”)。
(4)由本实验得到的数据作出小车的加速度a与弹簧测力计的示数F的关系图像，与本实验相符合的是__________。
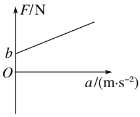
(5)若实验步骤②中，让长木板水平放置，没有做平衡摩擦力，其余实验步骤不变且操作正确，读出弹簧测力计的示数F，处理纸带，得到滑块运动的加速度a；改变钩码个数，重复实验，以弹簧测力计的示数F为纵坐标，以加速度a为横坐标，得到的图象是纵轴截距为b的一条倾斜直线，如图所示。已知小车的质量为M，重力加速度为g，忽略滑轮与绳之间的摩擦以及纸带与限位孔之间的摩擦，则小车和长木板之间的动摩擦因数μ＝__________。
【答案】C 0.88 偏小 A 
【解析】
(1)A.由图示实验装置可知，测力计可以测出细线对小车的拉力，实验不需要满足砝码的质量应远小于小车的质量，故A错误；
B.实验过程中砝码向下加速运动，砝码处于失重状态，故B错误；
C.为使小车受到的拉力等于细线的拉力，应调节滑轮的高度使与小车相连的轻绳与长木板一定要平行，故C正确；
D.实验过程中，砝码向下加速运动，处于失重状态，故弹簧测力计的读数小于砝码和砝码盘总重力的一半，故D错误。
(2)由图示纸带可知，相邻两个计数点之间的时间间隔：t=5×0.02 s=0.1 s，由匀变速直线运动的推论△x=at2，利用逐差法，可得加速度：a=（s3+s4-s1-s2）/4T2=0.88 m/s2。
(3)若交流电的实际频率大于50Hz，打点计时器打点的时间间隔小于0.02s，计数点间的时间间隔小于0.1s，计算加速度时所用时间t偏大，加速度的测量值小于真实值，即计算结果与实际值相比偏小。
(4)由图中所示装置及实验步骤可知，已经平衡好摩擦力，小车受到的拉力F可以由弹簧测力计测出，小车的加速度a与弹簧测力计的示数F的关系应该是成正比，即为过原点的一条倾斜直线，由图示可知，BCD错误A正确。
(5)滑块受到的拉力FT为弹簧测力计示数F，即：FT＝F，滑块受到的摩擦力为：f＝μMg，由牛顿第二定律可得：FT－f＝Ma，解得：F＝Ma＋μMg，由图象所给信息可得图象截距为：b＝μMg，解得：μ＝。
