题目内容
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )

| A.h | B.2h | C.3h | D.4h |

下降过程为自由落体运动,触地时两球速度相同,v=
,m2碰撞地之后,速度瞬间反向,大小相等,选m1与m2碰撞过程为研究过程,碰撞前后动量守恒,设碰后m1、m2速度大小分别为v1、v2,选向上方向为正方向,则:
m2v-m1v=m1v1+m2v2
由能量守恒定律得:
(m1+m2)v2=
+
m2
且,m2=3m1
联立解得:v1=2
反弹后高度为:H=
=4h
故选D
| 2gh |
m2v-m1v=m1v1+m2v2
由能量守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| m1v | 21 |
| 1 |
| 2 |
| v | 22 |
且,m2=3m1
联立解得:v1=2
| 2gh |
反弹后高度为:H=
| ||
| 2g |
故选D

练习册系列答案
相关题目
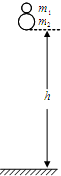 如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )


