题目内容
2.如图所示,足够长平行金属导轨内有垂直纸面向里的匀强磁场,金属杆ab与导轨垂直且接触良好,导轨右端通过电阻与平行金属板AB连接.已知导轨相距为L:磁场磁感应强度为B;R1、R2和ab杆的电阻值均为r,其余电阻不计;平行金属板AB间距为d、板长为4d、重力加速度为g,不计空气阻力.质量为m、带电量为+q的微粒以v0沿两板中心线水平射入,如果ab杆以某一速度向左匀速运动时,微粒恰能沿两板中心线射出;如果ab杆以同样大小的速度向右匀速运动时,该微粒将射到B板距左端为d的C处,如果以v0沿中心线射入的上述微粒能够从两板间射出,则ab杆向左匀速运动的速度可能为( )
| A. | $\frac{2mgd}{qBL}$ | B. | $\frac{21mgd}{8qBL}$ | C. | $\frac{3mgd}{qBL}$ | D. | $\frac{27mgd}{8qBL}$ |
分析 ab杆向左匀速运动时,电场力与重力方向相反,粒子做类平抛运动,要想使粒子射出电场水平位移应为L,同时竖直位移应该不小于$\frac{d}{2}$,棒速度较小则向下偏,较大则向上偏,讨论速度的范围
解答 解:带电量为+q的微粒恰能沿两板中心线射出,此时电场力与重力平衡,设场强为E,则:
mg=Eq…①
ab杆以同样大小的速度向右匀速运动时,平行板间带电粒子所受合力方向向下,大小为;
F=Eq+mg=2mg…②
粒子做类平抛运动,可知加速度为:
a=2g…③
打到板的时间为t,则:$\frac{d}{2}=\frac{1}{2}a{t}^{2}$…④
d=v0t…⑤
联立解得:v0=$\sqrt{2gd}$…⑥
ab杆向左匀速运动时,电场力与重力方向相反,棒速度较小则向下偏,较大则向上偏,粒子做类平抛运动,若粒子恰好射出电场,在水平位移应为L=4d时间内,同时竖直位移恰为$\frac{d}{2}$,
故粒子运动时间为:4d=v0t1…⑦
若向下偏,最小加速度大小为a1,则竖直方向位移为:$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}=\frac{d}{2}$…⑧
联立④⑤⑦⑧得:${a}_{1}=\frac{g}{8}$,
设此时导体棒速度最小为vmin,应有:a1=$\frac{mg-\frac{\frac{BL{v}_{min}}{3}}{d}q}{m}=g-\frac{BL{v}_{min}q}{3md}$,
解得:vmin=$\frac{21mgd}{8qBL}$,
若导体棒速度最大为vmax,此时粒子向上偏转,应有:${a}_{1}′={a}_{1}=\frac{\frac{\frac{BL{v}_{max}}{3}}{d}q-mg}{m}$=$\frac{BL{v}_{max}q}{3md}-g$,
解得:vmax=$\frac{27mgd}{8qBL}$.故BCD正确,A错误.
故选:BCD.
点评 本题考查电磁感应问题结合闭合电路欧姆定律,涉及带电粒子在匀强电场中的类平抛运动,运算量较大,有一定难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案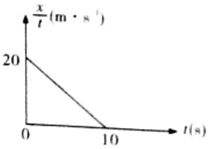
| A. | t=0时,物体初速度为10m/s | B. | 0~10s内物体运动方向未变 | ||
| C. | 0~10s内物体位移大小为0 | D. | 物体加速度大小为2m/s2 |
| A. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是轻核聚变 | |
| B. | X+${\;}_{7}^{14}$N→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H中,X表示${\;}_{2}^{3}$He | |
| C. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| D. | ${\;}_{90}^{232}$Th衰变成${\;}_{82}^{208}$Pb要经过6次α衰变和4次β衰变 |
| A. |  轴承间装滚珠 | B. |  写字时用力 | C. |  门轴加润滑油 | D. |  滑冰穿冰鞋 |
| A. | 牛顿发现了万有引力定律 | |
| B. | 随着科技的发展,地球同步卫星一定能出现在我国首都上空 | |
| C. | 滑动变阻器分压接法比限流接法的电压测量范围大 | |
| D. | 法拉第首先提出了电场的概念 |
| A. | 不存在电力 | |
| B. | 存在相互排斥力 | |
| C. | 存在相互吸引力 | |
| D. | 吸引力还是排斥力,取决于绝缘体带正电还是带负电 |
| A. | 受到的冲量大 | B. | 动量变化快 | C. | 动量变化量大 | D. | 受到的冲量小 |
| A. | 雷达卫星的线速度是动力环境卫星线速度的$\frac{1}{n}$ | |
| B. | 雷达卫星与动力环境卫星的向心加速度比$\frac{1}{{n}^{2}}$ | |
| C. | 在相同时间内,雷达卫星与动力环境卫星各自与地心的连线扫过的面积相等 | |
| D. | 雷达卫星与动力环境卫星的角速度之比$\frac{1}{{n}^{3}}$ |
