题目内容
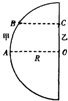
 如图所示,长为s的光滑水平面左端为竖直墙壁,右端与半径为R的光滑圆弧轨道相切于B点.一质量为m的小球从圆弧轨道上离水平面高为h(h<<R)的A点由静止开始下滑,则小球第一次运动到墙壁C点所需的时间为( )
如图所示,长为s的光滑水平面左端为竖直墙壁,右端与半径为R的光滑圆弧轨道相切于B点.一质量为m的小球从圆弧轨道上离水平面高为h(h<<R)的A点由静止开始下滑,则小球第一次运动到墙壁C点所需的时间为( )分析:h?R,可知小球在光滑圆弧上的运动为单摆运动,根据动能定理求出B点的速度,B到C做匀速直线运动,很容易求出B到C的时间,再根据周期公式求出A到B的时间,即可求出小球的运动周期.
解答:解:根据动能定理:mgh=
mv2-0,v=
,
B到C的时间:t1=
=
单摆的周期为:T=2π
,
所以A到B的时间:t2=
,
所以小球的运动周期为:T=(t1+t2)=
+s
.
故A正确,B、C、D错误.
故选A.
| 1 |
| 2 |
| 2gh |
B到C的时间:t1=
| s |
| v |
| s | ||
|
单摆的周期为:T=2π
|
所以A到B的时间:t2=
| π |
| 2 |
|
所以小球的运动周期为:T=(t1+t2)=
| π |
| 2 |
|
|
故A正确,B、C、D错误.
故选A.
点评:解决本题的关键知道什么样的运动是单摆运动,以及掌握单摆的周期公式T=2π
.
|

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
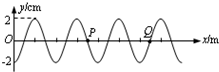
 A.某音叉的频率为440 Hz,示波器显示其稳定的图像如图,
A.某音叉的频率为440 Hz,示波器显示其稳定的图像如图, s
s 经若干次全反射后由B射出,经过测量,光在光导纤维内传播的最长时间为t,由此
经若干次全反射后由B射出,经过测量,光在光导纤维内传播的最长时间为t,由此


 A.某音叉的频率为440 Hz,示波器显示其稳定的图像如图,
A.某音叉的频率为440 Hz,示波器显示其稳定的图像如图, 经若干次全反射后由B射出,经过测量,光在光导纤维内传播的最长时间为t,由此
经若干次全反射后由B射出,经过测量,光在光导纤维内传播的最长时间为t,由此