题目内容
 水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是( )
水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是( )分析:力的方向由图象坐标的正负直接读出.根据牛顿第二定律和运动学公式结合求两个物体到达x=4m位置的时间.图象的“面积”大小等于力F所做的功,根据动能定理求出在x=8m的位置,A、B的动能.根据拉力与滑动摩擦力的关系分析两个物体最终的运动情况.
解答:解:
A、在x=4m到x=6m内,A、B两物体所受拉力都为正值,说明都沿正方向,方向相同.故A错误.
B、在x从0-4m内,根据牛顿第二定律得:
aA=
=2m/s2,aB=
=1m/s2.
由x=
aA
得,tA=2s;由x=v0tB+
aB
解得,tB=2s.故两物体同时到达x=4m的位置.故B正确.
C、根据图象的“面积”大小等于力F做功,得:两个拉力做功分别为:WA=6×4J+
×2J+4×2J=42J.
WB=1×4J+
×4J=22J,根据动能定理得
WA-μAmgx=EkA,得WA=32J,
WB-μBmgx=EkB-
m
,得WB=24J,故C错误.
D、两个物体所受的滑动摩擦力大小分别为fA=μAmg=4N,fB=μBmg=1N,由图判断可知,A做匀速直线运动,B做匀加速运动.故D错误.
故选B
A、在x=4m到x=6m内,A、B两物体所受拉力都为正值,说明都沿正方向,方向相同.故A错误.
B、在x从0-4m内,根据牛顿第二定律得:
aA=
| FA-μAmg |
| m |
| FB-μBmg |
| m |
由x=
| 1 |
| 2 |
| t | 2 A |
| 1 |
| 2 |
| t | 2 B |
C、根据图象的“面积”大小等于力F做功,得:两个拉力做功分别为:WA=6×4J+
| 6+4 |
| 2 |
WB=1×4J+
| 1+8 |
| 2 |
WA-μAmgx=EkA,得WA=32J,
WB-μBmgx=EkB-
| 1 |
| 2 |
| v | 2 0 |
D、两个物体所受的滑动摩擦力大小分别为fA=μAmg=4N,fB=μBmg=1N,由图判断可知,A做匀速直线运动,B做匀加速运动.故D错误.
故选B
点评:本题看似选择题,实质是计算题,根据牛顿第二定律、运动学公式和动能定理计算时间和物体的动能,要抓住图象的物理意义:面积表示力所做的功.

练习册系列答案
相关题目
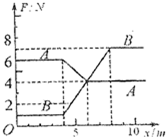 水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是
水平地面上并排放置A、B两个物体(都可视为质点),质量均为m=1kg,A物体的初速度为零,B的初速度为2m/s,A、B与地面的动摩擦因数分别为μA=0.4,μB=0.1,视滑动摩擦力与最大静摩擦力相等,重力加速度g取10m/s2,如图是这两个物体所受水平拉力F与位移x的关系,下列叙述正确的是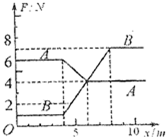
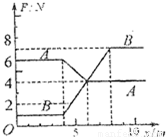
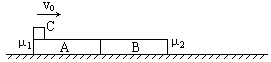 如图,两完全相同的木板A与B并排紧挨着放在水平地面上,在A的左端放置滑块C(C的大小不计).C与A、B的动摩擦因数均为μ1,A、B与水平地面间的动摩擦因数为μ2(A、B与水平地面间的最大静摩擦力与滑动摩擦力的大小相同).开始时C以初速度
如图,两完全相同的木板A与B并排紧挨着放在水平地面上,在A的左端放置滑块C(C的大小不计).C与A、B的动摩擦因数均为μ1,A、B与水平地面间的动摩擦因数为μ2(A、B与水平地面间的最大静摩擦力与滑动摩擦力的大小相同).开始时C以初速度