题目内容
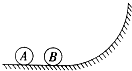 (2013?贵州模拟)如图所示,A、B两球放在光滑的水平面上,水平面的右侧与竖直平面内一光滑曲面相切,现给A一向右的速度,让A与B发生对心弹性碰撞,小球沿曲面上升到最高点后又能再沿曲面滑回到水平面.若要B返回水平面时能再与么发生碰撞,A、B的质量应满足什么关系?
(2013?贵州模拟)如图所示,A、B两球放在光滑的水平面上,水平面的右侧与竖直平面内一光滑曲面相切,现给A一向右的速度,让A与B发生对心弹性碰撞,小球沿曲面上升到最高点后又能再沿曲面滑回到水平面.若要B返回水平面时能再与么发生碰撞,A、B的质量应满足什么关系?分析:当A与B发生碰撞时,由动量守恒定律列出等式,由于A与B发生对心弹性碰撞,根据机械能守恒列出等式,
根据B返回水平面时能再与么发生碰撞得出A、B两球速度关系求解.
根据B返回水平面时能再与么发生碰撞得出A、B两球速度关系求解.
解答:解:设A、B的质量分别为mA和mB,设A的初速度为v0,
当A与B发生碰撞时,由动量守恒定律得:
mAv0=mAvA+mBvB ,
由于A与B发生对心弹性碰撞,根据机械能守恒得,
mA
=
mA
+
mB
解得:vA=
v0
vB=
v0
显然,如果二者碰撞后都向右运动或A停止运动,是一定能发生二次碰撞的,
在碰撞后A向左运动时,要能发生二次碰撞,需有:vB>-vA
解得:mA>
答:若要B返回水平面时能再与么发生碰撞,A、B的质量应满足mA>
当A与B发生碰撞时,由动量守恒定律得:
mAv0=mAvA+mBvB ,
由于A与B发生对心弹性碰撞,根据机械能守恒得,
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
解得:vA=
| mA-mB |
| mA+mB |
vB=
| 2mA |
| mA+mB |
显然,如果二者碰撞后都向右运动或A停止运动,是一定能发生二次碰撞的,
在碰撞后A向左运动时,要能发生二次碰撞,需有:vB>-vA
解得:mA>
| vB |
| 3 |
答:若要B返回水平面时能再与么发生碰撞,A、B的质量应满足mA>
| vB |
| 3 |
点评:解决该题关键要掌握碰撞过程中动量守恒及机械能守恒定律,即可正确解题,难度适中.

练习册系列答案
相关题目
 (2013?贵州模拟)课外活动中,某同学双手握在竖直放置的固定在地面的圆形器械上,如图所示.在手臂OA由水平方向缓慢移至A′位置的过程中,手臂OB不动.若手臂OA、OB的拉力分别为FA和FB,下列表述正确的是( )
(2013?贵州模拟)课外活动中,某同学双手握在竖直放置的固定在地面的圆形器械上,如图所示.在手臂OA由水平方向缓慢移至A′位置的过程中,手臂OB不动.若手臂OA、OB的拉力分别为FA和FB,下列表述正确的是( ) (2013?贵州模拟)某兴趣小组为探究测定电流产生磁场的磁感应强度的方法,在实验精度要求不高的情况下,设计了如下实验:在一根南北方向敢置的直导线的正下方A处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N吸)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已知此地的地磁场水平分量B=5.0×10-5T,通电后罗盘指针停在北偏东60°的位置,如图所示.由此得出该通电直导线在A处产生磁场的磁感应强度大小为( )
(2013?贵州模拟)某兴趣小组为探究测定电流产生磁场的磁感应强度的方法,在实验精度要求不高的情况下,设计了如下实验:在一根南北方向敢置的直导线的正下方A处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N吸)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已知此地的地磁场水平分量B=5.0×10-5T,通电后罗盘指针停在北偏东60°的位置,如图所示.由此得出该通电直导线在A处产生磁场的磁感应强度大小为( ) (2013?贵州模拟)如图所示,有一矩形线圈的面积为S,匝数为N,电阻不计,绕水平轴OO′在方向水平、磁感应强度为B的匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环接一理想降压变压器,滑动触头P上下移动时可改变输出电压,副线圈接有可变电阻R.以线框平面与磁场平行时为计时起点,下列判断正确的是( )
(2013?贵州模拟)如图所示,有一矩形线圈的面积为S,匝数为N,电阻不计,绕水平轴OO′在方向水平、磁感应强度为B的匀强磁场中以角速度ω匀速转动.矩形线圈通过滑环接一理想降压变压器,滑动触头P上下移动时可改变输出电压,副线圈接有可变电阻R.以线框平面与磁场平行时为计时起点,下列判断正确的是( )