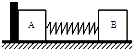
题目内容
| |||||||||||||||
解析:
(1) |
将A、B和弹簧看作系统,墙给A的冲量等于B的动量变化,I=mv. 由 所以IA=mv=4N·s.…………………………………………(4分) |
(2) |
A刚要离开墙时,弹簧为原长,系统只有动能.A、B交换速度是在A、B相互作用刚好结束时,总动能不变,所以弹性势能为零…………………………(4分) |
(3) |
在弹簧第一次恢复原长时,由 动量mBvB=2×2 mBvB=mBvB′+mAvA′ 代入数据得 4 在恢复原长时,无弹性势能,由机械能守恒,有 8= 代入数据得16=2vB′2+vA′2 ② ①②消去vA′得3vB′2-8 所以vB′= 第一组解:当vB′=2 第二组解:当vB′= 讨论:分析运动过程知,弹簧第一次恢复原长时,vA=0,vB=2 |


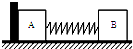 如图,A、B两物体用一根轻弹簧相连,放在光滑水平地面上,A物体左边有一竖直挡板.现用力向左推B压缩弹簧,然后突然撤去外力,B从静止开始向右运动,以后带动A做复杂运动,从A物体离开竖直挡板开始运动以后有( )
如图,A、B两物体用一根轻弹簧相连,放在光滑水平地面上,A物体左边有一竖直挡板.现用力向左推B压缩弹簧,然后突然撤去外力,B从静止开始向右运动,以后带动A做复杂运动,从A物体离开竖直挡板开始运动以后有( )