题目内容
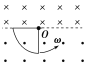
【题目】在直角坐标系xOy中,A(-0.3,0)、C是x轴上的两点,P点的坐标为(0,0.3)。在第二象限内以D(-0.3,0.3)为圆心、0.3m为半径的![]() 圆形区域内,分布着方向垂直xOy平面向外、磁感应强度大小为B=0.1T的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场。现有大量质量为m=3×10-9kg、电荷量为q=1×10-4C的相同粒子,从A点平行xOy平面以相同速率、沿不同方向射向磁场区域,其中沿AD方向射入的粒子从P点进入电场,经电场后恰好通过C点。已知α=37°,不考虑粒子间的相互作用及其重力,求:
圆形区域内,分布着方向垂直xOy平面向外、磁感应强度大小为B=0.1T的匀强磁场;在第一象限三角形OPC之外的区域,分布着沿y轴负方向的匀强电场。现有大量质量为m=3×10-9kg、电荷量为q=1×10-4C的相同粒子,从A点平行xOy平面以相同速率、沿不同方向射向磁场区域,其中沿AD方向射入的粒子从P点进入电场,经电场后恰好通过C点。已知α=37°,不考虑粒子间的相互作用及其重力,求:
(1)粒子的初速度大小;
(2)电场强度E的大小;
(3)粒子穿越x正半轴的最大横坐标。

【答案】(1)1×103m/s(2)112.5V/m(3)0.5m
【解析】
考查带电粒子在复合场中的运动。
(1)带电粒子在磁场中做匀速圆周运动,设半径r,粒子的初速度v
洛伦兹力提供向心力:
![]()
可得:![]()
根据题意和几何知识,可得:
r=DP=0.3m
代入上式得:v=1×103m/s;
(2)粒子轨迹圆的半径与速度垂直,所以沿AD方向的粒子由P点进入电场时,速度方向与y轴垂直,故该粒子在电场中做类平抛运动,设类平抛运动时间为t
x方向:
![]()
y方向:
![]()
根据几何关系得:
![]()
根据牛顿第二定律:
Eq=ma
联立各式得:E=112.5V/m ;
(3)

设速度方向与x轴正方向的夹角为θ的入射粒子,从x正半轴穿过时距离O点最远,粒子从F点离开磁场,其中O′是粒子运动轨迹的圆心,粒子运动到F点时的速度为vF,
由于粒子的运动半径等于磁场的半径,所以四边形ADFO′为菱形,O′F∥AD,速度vF⊥O′F,而AD又是竖直方向,所以vF垂直于y轴从F′点进入电场,仍做类平抛运动;
设粒子在电场中的运动时间为t′,粒子穿越x正半轴的最大坐标为![]() ,粒子做类平抛运动x方向的位移为x,F′点的坐标为(
,粒子做类平抛运动x方向的位移为x,F′点的坐标为(![]() ,
,![]() ),F点的纵坐标为yF,则:
),F点的纵坐标为yF,则:
![]()
类平抛过程,x方向:
x=vt′
y方向:
![]()
粒子到达x轴的坐标为:
![]()
根据几何关系得:
![]()
![]()
联立各式,得:
![]()
令![]() =k,所以:
=k,所以:
![]()
根据数学知识可知,当k=0.5时![]() 有最大值,最大值为0.5m。
有最大值,最大值为0.5m。

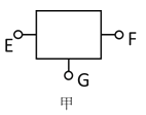
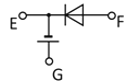
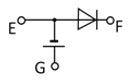
【题目】如图所示是欧姆表的原理图,灵敏电流表的满偏电流为![]() ,干电池的电动势为1.5V.
,干电池的电动势为1.5V.

(1)把灵敏电流表的电流刻度值对应的欧姆表的电阻刻度值填在下表中______.
电流刻度/ | 0 | 100 | 200 | 250 | 300 | 400 | 500 |
电阻刻度/ |
(2)这个欧姆表的内阻是__________![]() ,表针偏转到满偏刻度的
,表针偏转到满偏刻度的![]() 处时,待测电阻值为_______
处时,待测电阻值为_______![]() .
.
(3)若欧姆表内的电池用久了,电动势降为1.4V,欧姆表的内阻变为_________![]() ,若此时测某电阻
,若此时测某电阻![]() ,电表指针恰好指在中央位置,则
,电表指针恰好指在中央位置,则![]() 的实际值为________
的实际值为________![]() ,比从原表盘上读出的阻值要偏________(填“大”或“小”).
,比从原表盘上读出的阻值要偏________(填“大”或“小”).