题目内容
 在真空中由阴极K发射出电子,其初速度可忽略不计,此电子经加速电场加速后从偏转电场的中线垂直进入,然后打到一光屏上.已知,电子的电量为q,质量为m,加速电场的电压为∪1,偏转电场的电压为∪2,板长为L1,两板间距为d,偏转电场的右边缘到屏的距离为L2,试求:
在真空中由阴极K发射出电子,其初速度可忽略不计,此电子经加速电场加速后从偏转电场的中线垂直进入,然后打到一光屏上.已知,电子的电量为q,质量为m,加速电场的电压为∪1,偏转电场的电压为∪2,板长为L1,两板间距为d,偏转电场的右边缘到屏的距离为L2,试求:(1)电子打到屏上时的速度为多大.
(2)电子打到屏上的点到O点的距离.
分析:(1)电子先经加速电场加速,再经偏转电场偏转.先根据动能定理得到加速获得的速度表达式.运用运动的分解法,由牛顿第二定律和运动学公式得到电子偏转的距离,由速度合成求出电子离开电场时的速度,即为电子打到屏上时的速度.
(2)电子离开电场后做匀速直线运动,由数学知识求得电子打到屏上的点到O点的距离.
(2)电子离开电场后做匀速直线运动,由数学知识求得电子打到屏上的点到O点的距离.
解答:解:在加速电场中,根据动能定理得:qU1=
m
…①
在偏转电场中,设偏转距离为y,偏转角度为θ,则有:
L1=v0t
y=
at2
tanθ=
=
又加速度a=
联立得:tanθ=
,y=
(1)电子打到屏上时的速度v=
=
=
=
(2)电子打到屏上的点到O点的距离y′=y+L2tanθ=
+L2?
=
(L1+2L2).
答:
(1)电子打到屏上时的速度为
.
(2)电子打到屏上的点到O点的距离是
(L1+2L2).
| 1 |
| 2 |
| v | 2 0 |
在偏转电场中,设偏转距离为y,偏转角度为θ,则有:
L1=v0t
y=
| 1 |
| 2 |
tanθ=
| vy |
| v0 |
| at |
| v0 |
又加速度a=
| qU2 |
| md |
联立得:tanθ=
| U2L1 |
| 2U1d |
U2
| ||
| 4U1d |
(1)电子打到屏上时的速度v=
|
|
|
|
(2)电子打到屏上的点到O点的距离y′=y+L2tanθ=
U2
| ||
| 4U1d |
| U2L1 |
| 2U1d |
| U2L1 |
| 4dU1 |
答:
(1)电子打到屏上时的速度为
|
(2)电子打到屏上的点到O点的距离是
| U2L1 |
| 4dU1 |
点评:解决本题的关键知道电子的运动规律,现在加速电场中加速,然后进入偏转电场做类平抛运动,离开偏转电场做匀速直线运动.

练习册系列答案
相关题目
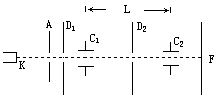

 方向偏转的电极)所示。电子束打在荧光屏上形成光迹。这三部分均封装于真空玻璃壳中。已知电子的电荷量
方向偏转的电极)所示。电子束打在荧光屏上形成光迹。这三部分均封装于真空玻璃壳中。已知电子的电荷量 =1.6×10
=1.6×10 C,质量
C,质量 =9.0×10
=9.0×10 kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
 为多大;
为多大; =4cm,两板间距离
=4cm,两板间距离 =1cm,Y极板右端与荧光屏的距离
=1cm,Y极板右端与荧光屏的距离 =18cm,当在偏转电极上加
=18cm,当在偏转电极上加 的正弦交变电压时,如果电子进入偏转电场的初速度
的正弦交变电压时,如果电子进入偏转电场的初速度 ,每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场。求电子打在荧光屏上产生亮线的最大长度;
,每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场。求电子打在荧光屏上产生亮线的最大长度; 方向偏转的电极)所示。电子束打在荧光屏上形成光迹。这三部分均封装于真空玻璃壳中。已知电子的电荷量
方向偏转的电极)所示。电子束打在荧光屏上形成光迹。这三部分均封装于真空玻璃壳中。已知电子的电荷量 =1.6×10
=1.6×10 C,质量
C,质量 =9.0×10
=9.0×10 kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
kg,电子所受重力及电子之间的相互作用力均可忽略不计,不考虑相对论效应。
 为多大;
为多大; =4cm,两板间距离
=4cm,两板间距离 =1cm,Y极板右端与荧光屏的距离
=1cm,Y极板右端与荧光屏的距离 =18cm,当在偏转电极上加
=18cm,当在偏转电极上加 的正弦交变电压时,如果电子进入偏转电场的初速度
的正弦交变电压时,如果电子进入偏转电场的初速度 ,每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场。求电子打在荧光屏上产生亮线的最大长度;
,每个电子通过偏转电场的过程中,电场可视为稳定的匀强电场。求电子打在荧光屏上产生亮线的最大长度;