Question

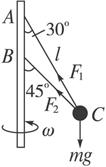
如图6—8—30所示，水平转盘的中心有个竖直小圆筒，质量为m的物体A放在转盘上，A到竖直筒中心的距离为r，物体A通过轻绳、无摩擦的滑轮与物体B相连，B与A质量相同，物体A与盘间的最大静摩擦力是压力的μ倍，则转盘转动的角速度在什么范围内，物体A才能随盘转动？

Answer 1

≤ω≤

解析:

由于A在圆盘上随盘做匀速圆周运动，所以它所受的合外力必然指向圆心，而其中重力、支持力平衡，绳的拉力指向圆心，所以A所受的摩擦力的方向一定沿着半径指向圆心或背离圆心。

当A将要沿盘向外滑时，A所受的最大静摩擦力指向圆心，A的向心力为绳的拉力与最大静摩擦力的合力。即F+F_m= m rω₁²   ①  由于B静止，故F=mg ，   ②由于最大静摩擦力是压力的μ倍，即F_m=μF_N =μmg  ③ 由①②③解得ω₁=；当A将要沿盘向圆心滑时，A所受的最大静摩擦力沿半径向外，这时向心力为：F-F_m= mω₂²r  ④，由②③④得ω₂=   要使A随盘一起转动，其角速度ω应满足≤ω≤