题目内容
A、B两小球同时从距地面高h=15m处的同一点抛出，初速度大小均为v=10m/s．A球竖直向下抛出，B球水平抛出，空气阻力不计，重力加速度取g=l0m/s2．求：（1）A球经多长时间落地？
（2）A球落地时，A、B两球间的距离是多少？
【答案】分析：（1）A球做匀加速直线运动，根据位移时间公式直接求解；
（2）B球做平抛运动，A球落地时间内，分别求出B球的水平分位移和竖直分位移，然后根据空间关系，得出A、B两球间的距离．
解答：解：（1）A球做竖直下抛运动：
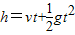
将h=15m．v=10m/s代入，可得：
t=1s
即A球经1s时间落地．
（2）B球做平抛运动：
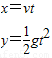
将v=10m/s．t=1s代入，可得：
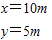
此时A球与B球的距离L为：
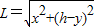
将x．y．h代入，得：
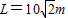
即A、B两球间的距离是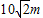
．
点评：本题关键是分清两球的运动规律，同时结合空间位置情况，运用运动学公式求解．
（2）B球做平抛运动，A球落地时间内，分别求出B球的水平分位移和竖直分位移，然后根据空间关系，得出A、B两球间的距离．
解答：解：（1）A球做竖直下抛运动：
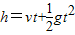
将h=15m．v=10m/s代入，可得：
t=1s
即A球经1s时间落地．
（2）B球做平抛运动：
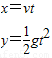
将v=10m/s．t=1s代入，可得：
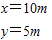
此时A球与B球的距离L为：
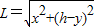
将x．y．h代入，得：
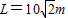
即A、B两球间的距离是
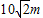．点评：本题关键是分清两球的运动规律，同时结合空间位置情况，运用运动学公式求解．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目