题目内容
如图所示,某透明液体深1m,一束与水平面成30°角的光线从空气射向该液体,进入该液体的光线与水平面的夹角为45°.试求:(1)该液体的折射率;
(2)进入液体的光线经多长时间可以照到底面.
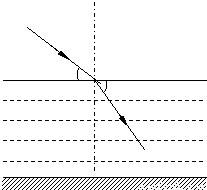
【答案】分析:(1)由题,已知入射角i=60°,折射角r=45°,根据折射定律求解该液体的折射率;
(2)由几何知识求出光在液体中传播的距离S,由v=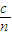 求出光在液体中传播的速度v,根据公式t=
求出光在液体中传播的速度v,根据公式t= 求出时间.
求出时间.
解答:解:
(1)根据几何知识可知,入射角i=60°,折射角r=45°,根据折射定律得
n=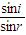 =
=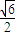
(2)光在液体中传播的速度v=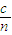 =
=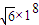 m/s
m/s
传播的距离S=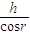 =
=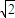 m
m
所以t= =
=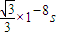
答:(1)该液体的折射率是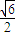 ;
;
(2)进入液体的光线经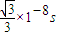 照到底面.
照到底面.
点评:本题是几何光学中基本问题,是n=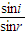 和v=
和v=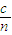 的综合应用,比较简单.
的综合应用,比较简单.
(2)由几何知识求出光在液体中传播的距离S,由v=
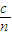 求出光在液体中传播的速度v,根据公式t=
求出光在液体中传播的速度v,根据公式t= 求出时间.
求出时间.解答:解:
(1)根据几何知识可知,入射角i=60°,折射角r=45°,根据折射定律得
n=
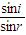 =
=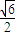
(2)光在液体中传播的速度v=
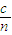 =
=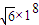 m/s
m/s传播的距离S=
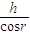 =
=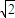 m
m所以t=
 =
=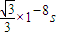
答:(1)该液体的折射率是
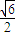 ;
;(2)进入液体的光线经
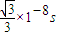 照到底面.
照到底面.点评:本题是几何光学中基本问题,是n=
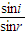 和v=
和v=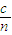 的综合应用,比较简单.
的综合应用,比较简单. 
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 (2007?徐州模拟)如图所示,某透明液体深1m,一束与水平面成30°角的光线从空气射向该液体,进入该液体的光线与水平面的夹角为45°.试求:
(2007?徐州模拟)如图所示,某透明液体深1m,一束与水平面成30°角的光线从空气射向该液体,进入该液体的光线与水平面的夹角为45°.试求:

