题目内容
 (2009?滨州模拟)下图是质谱仪工作原理的示意图.带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,则( )
(2009?滨州模拟)下图是质谱仪工作原理的示意图.带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,则( )分析:带电粒子先在匀强电场中做匀加速直线运动,再进入磁场做匀速圆周运动,轨迹为半圆,本题动能定理和牛顿第二定律求解.
解答:解:设粒子经电场加速后的速度大小为v,磁场中圆周运动的半径为r,电荷量和质量分别为q、m,打在感光板上的距离为S.
根据动能定理,得
qU=
mv2,v=
由qvB=m
,r=
=
则S=2r=
得到
=
由图,Sa<Sb,U、B相同,则
>
故选D
根据动能定理,得
qU=
| 1 |
| 2 |
|
由qvB=m
| v2 |
| r |
| mv |
| qB |
| 1 |
| B |
|
则S=2r=
| 2 |
| B |
|
得到
| q |
| m |
| 8U |
| BS2 |
由图,Sa<Sb,U、B相同,则
| qa |
| ma |
| qb |
| mb |
故选D
点评:本题属于带电粒子在组合场中运动问题,电场中往往用动能求速度,磁场中圆周运动处理的基本方法是画轨迹.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
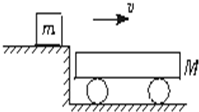 (2009?滨州模拟)如图所示,木块质量m=0.4kg,它以速度v=20m/s水平地滑上一辆静止的平板小车,已知小车质量M=1.6kg,木块与小车间的动摩擦因数为μ=0.2,木块没有滑离小车,地面光滑,g取10m/s2.
(2009?滨州模拟)如图所示,木块质量m=0.4kg,它以速度v=20m/s水平地滑上一辆静止的平板小车,已知小车质量M=1.6kg,木块与小车间的动摩擦因数为μ=0.2,木块没有滑离小车,地面光滑,g取10m/s2. (2009?滨州模拟)如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是 ( )
(2009?滨州模拟)如图所示,倾角为30°,重为80N的斜面体静止在水平面上.一根弹性轻杆一端垂直固定在斜面体上,杆的另一端固定一个重为2N的小球,小球处于静止状态时,下列说法正确的是 ( ) (2009?滨州模拟)(1)某运动员吸一口气,吸进400cm3的空气,据此估算他所吸进的空气分子的总数.已知1mol气体处于标准状态时的体积是22.4L.(结果保留一位有效数字)
(2009?滨州模拟)(1)某运动员吸一口气,吸进400cm3的空气,据此估算他所吸进的空气分子的总数.已知1mol气体处于标准状态时的体积是22.4L.(结果保留一位有效数字)