��Ŀ����
ij��ȤС�������һ��ʵ��װ�ã������о���ײ���⣬��ģ����ͼ��ʾ������ȫ��ͬ��������N����С��ͬ���������ȵ�С����������һˮƽ�ˡ������С����������ң���ı������Ϊ1��2��3��N������������εݼ���ÿ����������������������֮��Ϊk��k��1������1������������Ȼ���ɾ�ֹ�ͷţ�ʹ����2������ײ��2��������3������ײ��������ײ��Ϊ��е����ʧ�������������ƿ������������������쳤��gȡ10m/s2��
��1������n+1������ײǰ��n������ٶ�Ϊvn����n+1������ײ����ٶȣ�
��2����N=5����1������������h������£�Ҫʹ5������ײ������16k��16hС����������kֵΪ���٣�
��1������n+1������ײǰ��n������ٶ�Ϊvn����n+1������ײ����ٶȣ�
��2����N=5����1������������h������£�Ҫʹ5������ײ������16k��16hС����������kֵΪ���٣�

��1�������е��������������ɿ����ǡ�һ��һ��������ײģ�͡�����Ϊÿ������������εݼ������������������������������������Ϊm1������������Ϊm2����ǰm1���ٶ�Ϊv1������������ٶȷֱ�Ϊv1�䡢v2���ɶ����غ㶨�ɺͻ�е���غ㶨�ɵã�
m v1=m1v1��+m2v2��
mV12=
mV��12+
mV��22
�ã�V��1=
V1 V��2=
V1
������ҪӦ��v2�䵱nȡ��1ʱ��n+1��ȡ��2��
��n��������Ϊm����n+1������ײ����ٶȷֱ�Ϊvn�䡢vn+1��ȡˮƽ����Ϊ������������n������n+1������ײǰ���ٶȷֱ�Ϊvn��0��mn+1=kmn
���ݶ����غ㣬��mnVn=mnV��n+kmnV��n+1����
���ݻ�е���غ㣬��
mnVn2=
mnV��n2+
kmnV��n+12����
�ɢ٢ڵã�V��n+1=
(V��n+1=0��ȥ)����
��2����1���������͵�ʱ���ٶ�Ϊv1���ɻ�е���غ㶨���У�
m1gh=
m1V12����
v1=
����
ͬ������5��������˲����ٶ�
V5=
����
�ɢ�ʽ�ɵ�Vn+1= (
)nv1����
N=n=5ʱ��v5=(
)5V1����
�ɢݢޢ���ʽ�ã�
k=
-1=0.414����
�𣺣�1��n+1������ײ����ٶ�V��n+1=
��2��kֵΪ0.414
m v1=m1v1��+m2v2��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�ã�V��1=
| m1-m2 |
| m1+m2 |
| 2 m1 |
| m1+m2 |
������ҪӦ��v2�䵱nȡ��1ʱ��n+1��ȡ��2��
��n��������Ϊm����n+1������ײ����ٶȷֱ�Ϊvn�䡢vn+1��ȡˮƽ����Ϊ������������n������n+1������ײǰ���ٶȷֱ�Ϊvn��0��mn+1=kmn
���ݶ����غ㣬��mnVn=mnV��n+kmnV��n+1����
���ݻ�е���غ㣬��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�ɢ٢ڵã�V��n+1=
| 2Vn |
| k+1 |
��2����1���������͵�ʱ���ٶ�Ϊv1���ɻ�е���غ㶨���У�
m1gh=
| 1 |
| 2 |
v1=
| 2gh |
ͬ������5��������˲����ٶ�
V5=
| 2g��16k |
�ɢ�ʽ�ɵ�Vn+1= (
| 2 |
| 1+k |
N=n=5ʱ��v5=(
| 2 |
| 1+k |
�ɢݢޢ���ʽ�ã�
k=
| 2 |
�𣺣�1��n+1������ײ����ٶ�V��n+1=
| 2Vn |
| k+1 |
��2��kֵΪ0.414

��ϰ��ϵ�д�
 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
�����Ŀ
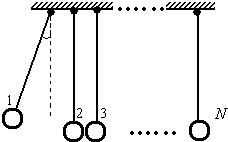 ij��ȤС�������һ��ʵ��װ�ã������о���ײ���⣬��ģ����ͼ��ʾ������ȫ��ͬ��������N����С��ͬ���������ȵ�С����������һˮƽ�ˡ������С����������ң���ı������Ϊ1��2��3��N������������εݼ���ÿ����������������������֮��Ϊk��k��1������1������������Ȼ���ɾ�ֹ�ͷţ�ʹ����2������ײ��2��������3������ײ��������ײ��Ϊ��е����ʧ�������������ƿ������������������쳤��gȡ10m/s2��
ij��ȤС�������һ��ʵ��װ�ã������о���ײ���⣬��ģ����ͼ��ʾ������ȫ��ͬ��������N����С��ͬ���������ȵ�С����������һˮƽ�ˡ������С����������ң���ı������Ϊ1��2��3��N������������εݼ���ÿ����������������������֮��Ϊk��k��1������1������������Ȼ���ɾ�ֹ�ͷţ�ʹ����2������ײ��2��������3������ײ��������ײ��Ϊ��е����ʧ�������������ƿ������������������쳤��gȡ10m/s2�� ��2012?���գ�ij��ȤС�������һ�ַ���װ�ã���ͼ��ʾ���ڴż���Բ��״��о֮���γɵ����ų������Բ�ĽǦ���Ϊ
��2012?���գ�ij��ȤС�������һ�ַ���װ�ã���ͼ��ʾ���ڴż���Բ��״��о֮���γɵ����ų������Բ�ĽǦ���Ϊ �У��ų����ذ뾶��������ΪN�ľ�����Ȧ��abcd�ı߳�ab��cd��l��bc��ad��2l.��Ȧ�Խ��ٶ���������������ת����bc��ad��ͬʱ����ų����ڴų��У����������������ĴŸ�Ӧǿ�ȴ�С��ΪB������ʼ���������ߵ��˶�����ֱ����Ȧ���ܵ���Ϊr����ӵ���ΪR.��
�У��ų����ذ뾶��������ΪN�ľ�����Ȧ��abcd�ı߳�ab��cd��l��bc��ad��2l.��Ȧ�Խ��ٶ���������������ת����bc��ad��ͬʱ����ų����ڴų��У����������������ĴŸ�Ӧǿ�ȴ�С��ΪB������ʼ���������ߵ��˶�����ֱ����Ȧ���ܵ���Ϊr����ӵ���ΪR.��
