题目内容

如图所示，小明同学正在进行滑板运动．图中AB段路面是水平的，BCD是一段R=20m的拱起的圆弧路面，圆弧的最高点C比AB的高出h=1.25m．已知人与滑板的总质量为M=60kg．小明自A点由静止开始运动，在AB路段他单腿用力蹬地，到达B点前停止蹬地，然后冲上圆弧路段，结果到达C点时恰好对地面压力为零，不计滑板与各路段之间的摩擦力及经过B点时的能量损失．求小明在AB段所做的功．（g取10m/s2）
分析：人和滑板在圆弧的最高点，靠重力提供向心力，根据牛顿第二定律求出最高点的速度，通过机械能守恒定律求出B点的速度，再通过动能定理求出小明在AB段所做的功．
解答：解：人和滑板在半径为R的圆周上作圆周运动，处于圆周轨道的最高点时所受重力提供向心力，设滑行到C点时的速度为vC，根据牛顿第二定律
Mg=M
vC2
R
  
得vC=10
2
m/s
人和滑板从水平面运动到C的过程中，根据机械能守恒定律得
1
2
MvB2=
1
2
MvC2+Mgh  
解得vB=15m/s．
在AB段用动能定理得
W=
1
2
MvB2=6750J
答：小明在AB段所做的功为6750J．
点评：本题综合考查了牛顿第二定律、动能定理和机械能守恒定律，难度不大，需加强这类题型的训练．
练习册系列答案
相关题目
某校组织高一学生外出举行“校园文化游”活动．坐在行驶的火车上时，物理老师问同学们：“假设此时火车的运动可近似看成匀加速直线运动，哪一位同学能运用身边的物品，估测出火车的加速度呢？”小明和小丽两同学最先用正确的方法估测出了加速度．他们的测定方法如下：
①小明利用一把小铁锁做实验进行估测，他的方法是：用塑料绳把一只小铁锁（可看成质点）吊起来，并悬挂在行李架上，使悬挂点正好在小桌边缘的正上方（如图所示），用刻度尺测出塑料绳的悬挂点到小铁锁的距离L、小铁锁偏离后离桌子的竖直高度h和水平距离s，通过计算便可估测出列车的加速度；
②小丽同学则是利用铁路两旁的电线杆来进行观察和测算，
她的方法是：用手表估测出火车从第一根电线杆到第二根电
线杆的时间t1，从第二根到第三根的时间t2，若已知相邻两根电线杆的间距均为s，则通过计算也可估测出列车的加速度．
现在请你运用运动学和牛顿运动定律的有关知识并根据两位同学的测定方法分别推算出列车运动的加速度a表达式．
（2007?广东）某研究性学习小组发现河水在缓慢流动时有一个规律，河中央流速最大，岸边速度几乎为零．为了研究河水流速与从岸边到中央距离的关系，小明同学设计了这样的测量仪器：如图甲所示，两端开口的“L”型玻璃管的水平部分置于待测的水流中，竖直部分露出水面，且露出水面部分的玻璃管足够长．当水流以速度 v 正对“L”型玻璃管的水平部分开口端匀速流动时，管内外液面的高度差为 h，且h 随水流速度的增大而增大．为了进一步研究水流速度v 与管内外水面高度差h的关系，该组同学进行了定量研究，得到了如下的实验数据，并根据实验数据得到了v-h 图象，如图丙所示．

v（m/s） 0 1.00 1.41 1.73 2.00 2.45 3.00 3.16
h（m） 0 0.05 0.10 0.15 0.20 0.30 0.45 0.50
（1）根据根据上表的数据和图丙中图象的形状，可猜想v和h之间的关系为
v2=20h
v2=20h
；为验证猜，请在图丁中确定纵轴所表示的物理量，并另作 图象，若该图象的形状为
直线
直线
，说明猜想正确．

（2）现利用上述测速器，由河流南岸开始，每隔1米测一次流速，得到数据如下表所示：
测试点距岸距离 x/m 0 1 2 3 4 5 6
管内外高度差   h/cm 0 0.8 3.2 7.2 12.8 20.0 28.8
相应的水流速度 v/ms-1
0
0
0.4
0.4
0.8
0.8
1.2
1.2
1.6
1.6
2.0
2.0
2.4
2.4
根据v和h之间的关系完成上表的最后一行，对比上表中的数据，可以看出河中水流速度 v 与从南岸到河流中央距离x的关系为：
v=0.4x
v=0.4x
．
某研究性学习小组发现河水在缓慢流动时有一个规律，河中央流速最大，岸边速度几乎为零．为了研究河水流速与从岸边到中央距离的关系，小明同学设计了这样的测量仪器：如图甲所示，两端开口的“L”型玻璃管的水平部分置于待测的水流中，竖直部分露出水面，且露出水面部分的玻璃管足够长．当水流以速度 v 正对“L”型玻璃管的水平部分开口端匀速流动时，管内外液面的高度差为 h，且h 随水流速度的增大而增大．为了进一步研究水流速度v 与管内外水面高度差h的关系，该组同学进行了定量研究，得到了如下的实验数据，并根据实验数据得到了v-h 图象，如图丙所示．
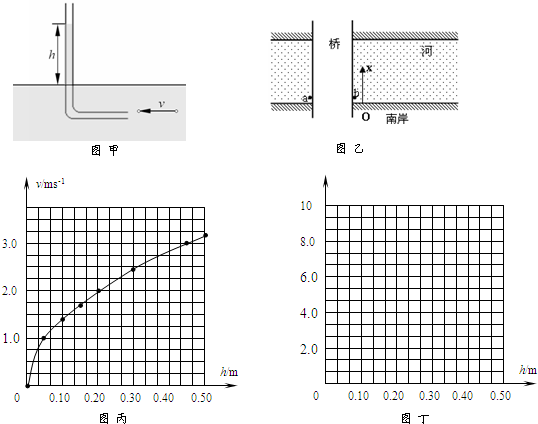
精英家教网
v（m/s） 0 1.00 1.41 1.73 2.00 2.45 3.00 3.16
h（m） 0 0.05 0.10 0.15 0.20 0.30 0.45 0.50
（1）根据根据上表的数据和图丙中图象的形状，可猜想v和h之间的关系为
 
；为验证猜想，图丁的纵坐标应设定为
 
，并另作图象，若该图象的形状为
 
，说明猜想正确．
（2）现利用上述测速器，由河流南岸开始，每隔1米测一次流速，得到数据如下表所示：
测试点距南岸距离 x/m 0 1 2 3 4 5 6 7
管内外液面高度差   h/cm 0 0.8 3.2 7.2 12.8 20.0 18.1 11.2
相应的水流速度 v/ms-1
分析对比上表中的数据，可以看出河中水流速度 v 与从观测点距离南岸的距离x的关系为：
 
．该河流中水流的最大流速约为
 
m/s．
（1）光电计时器由光电门和计时器两部分组成，如图甲所示精英家教网，此装置能较精确地记录物体通过光电门所用的时间．现要用此装置来验证机械能守恒定律，有一小球从两光电门的正上方静止释放，如图乙所示．（已知当地重力加速度为g）
①实验中除了需要测量小球直径D和小球通过两光电门l、2的时间△t1和△t2外，还需测量
 
（所测物理量用字母表示并用文字说明）．
②本实验需验证的关系式为
 
．（用上述已测物理量字母表示）
③为了减小实验误差，请你提出一条合理化的建议
 
．
（2）小明同学使用了以下器材测量某蓄电池的电动势E和内电阻r
A．待测的蓄电池（电动势约为2V）
B．电压表V（量程3V，内阻约为3kΩ）
C．电阻箱R（0～999.9Ω）精英家教网
D．定值电阻R0（R=2Ω）
E．开关S和导线若干
①由于待测蓄电池的内阻很小，当改变电阻箱的阻值，为保证电压表的示数变化较为明显，请在右图甲中用笔画线代替导线，将实验电路实物图连接完整．
②小明同学按其设计的实验电路正确操作，记录电阻箱的阻值和对应的电压表的读数U，计算出
U
R
的数值，得到多组数据并以为U为纵坐标，
U
R
为横坐标，将数据描在图乙所示的坐标纸上；请在图乙中完成U-
U
R
图线，利用图线求出蓄电池的电动势E=
 
V，内阻r=
 
Ω．
③若考虑电压表内阻对电动势测量结果的影响，则电动势的测量值E测和真实值E真的关系是E测
 
E真（填“大于”、“小于”或“等于”）．

某校组织高一学生外出举行“校园文化游”活动．坐在行驶的火车上时，物理老师问同学们：“假设此时火车的运动可近似看成匀加速直线运动，哪一位同学能运用身边的物品，估测出火车的加速度呢？”小明和小丽两同学最先用正确的方法估测出了加速度．他们的测定方法如下：
①小明利用一把小铁锁做实验进行估测，他的方法是：用塑料绳把一只小铁锁（可看成质点）吊起来，并悬挂在行李架上，使悬挂点正好在小桌边缘的正上方（如图所示），用刻度尺测出塑料绳的悬挂点到小铁锁的距离L、小铁锁偏离后离桌子的竖直高度h和水平距离s，通过计算便可估测出列车的加速度；
②小丽同学则是利用铁路两旁的电线杆来进行观察和测算，
她的方法是：用手表估测出火车从第一根电线杆到第二根电
线杆的时间t1，从第二根到第三根的时间t2，若已知相邻两根电线杆的间距均为s，则通过计算也可估测出列车的加速度．
现在请你运用运动学和牛顿运动定律的有关知识并根据两位同学的测定方法分别推算出列车运动的加速度a表达式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网