题目内容
如图所示,质量M=4kg长为L=1Om的木板停放在光滑水平面上,另一不计长度质量m=1kg的木块以某一速度从右端滑上木板,木板与木块间的动摩擦因数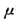 =0.8.若要使木板获得的速度不大于2m/S,木块的初速度V0应满足的条件为(g取10m/s2)( )
=0.8.若要使木板获得的速度不大于2m/S,木块的初速度V0应满足的条件为(g取10m/s2)( )
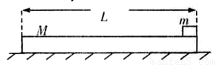
A.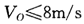 B.
B.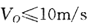
C.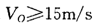 D.
D.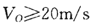
【答案】
BC
【解析】
试题分析: 木块在木板上滑动时,木块的加速度a1=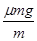 =8m/s,木板的加速度a2=
=8m/s,木板的加速度a2=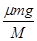 =
m/s,若木块最终从左端离开木板,则此过程中木板一直做匀加速运动,木块离开时,木板速度最大,则有v2≤2m/s,所以t≤
=
m/s,若木块最终从左端离开木板,则此过程中木板一直做匀加速运动,木块离开时,木板速度最大,则有v2≤2m/s,所以t≤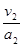 =1s,木块一直做匀减速运动,则有:x木块-x木板=10m
=1s,木块一直做匀减速运动,则有:x木块-x木板=10m
即v0t+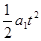 -
-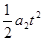 =10m,带入数据解得:v0≥15m/s
=10m,带入数据解得:v0≥15m/s
若木块先减速后和木板一起匀速运动,根据动量守恒定律得:
mv0=(m+M)v,解得:v0=5v,因为v≤2m/s,所以v0≤10m/s。故选BC
考点:牛顿第二定律;动量守恒定律;匀变速直线运动规律。

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求:
如图所示,质量m=4.0kg的物体与地面的动摩擦因数μ=0.50,物体在与地面成θ=37°的恒力F作用下,由静止开始运动,运动0.20s撤去F,又经过0.40s物体刚好停下.(sin37°=0.60)求: 如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求:
如图所示,质量M=4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m=1.0kg的小滑块A(可视为质点).初始时刻,A、B分别以v0=2.0m/s向左、向右运动,最后A恰好没有滑离B板.已知A、B之间的动摩擦因数μ=0.40,取g=10m/s2.求: (2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求:
(2011?重庆一模)如图所示,质量M=4.0kg的滑板B静止于光滑的水平面上.滑板右端固定着一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5m,在L=0.5m这一段滑板上B与木块A之间的动摩擦因数μ=0.2,而弹簧的自由端C到弹簧固定端D所对应的滑板上表面光滑.可视为质点的木块A质量m=1.0kg,静止于滑板的左端.滑板B受水平向左的恒力F=14.0N,作用一定时间后撤去该力,此时木块A恰好运动到滑板C处(g取10.0m/s2).试求: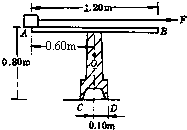 质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少?
质量M=2.0kg的小铁块静止于水平轨道AB的A端.导轨及支架ABCD形状及尺寸如图所示,质量m=4.0kg.它只能绕通过支架D点垂直于纸面水平转动,其中心在图中的O点,现有一细线沿导轨拉小铁块,拉力F=12N,小铁块和导轨之间的动摩擦因数μ=0.50.g取10m/s2从小铁块运动时起,导轨(及支架)能保持静止的最长时间是多少? 如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.
如图所示,质量M=4.0kg,长L=4.0m的木板B静止在光滑水平地面上,木板右端与竖直墙壁之间距离为s=6.0m,其上表面正中央放置一个质量m=1.0kg的小滑块A,A与B之间的动摩擦因数μ=0.2.现用大小为F=18N的推力水平向右推B,两者发生相对滑动,作用1s后撤去推力F,通过计算可知,在B与墙壁碰撞时A没有滑离B.设B与墙壁碰撞时间极短,且无机械能损失,重力加速度g=10m/s2.求A在B上滑动的整个过程中,A,B系统因摩擦产生的内能增量.