题目内容
如图所示，两条垂直于AB面的光线入射到折射率为| 2 |
30°
30°
．分析：作出光路图，由几何知识得到两条光线射到右侧面时的入射角，由折射定律求出折射角．再根据几何知识求解两条出射光线之间的夹角．
解答：解：作出光路图．由几何知识可知，上面一条光线从棱镜内射向右侧面时的入射角i=30°，
根据折射定律得n=
，得sinr=nsini=
×sin30°=
，则r=45°，
同理可知，第二条出射光线的折射角也是45°，
从图中的四边形可求出α=360°-120°-90°-90°=60°，
β=360°-135°-135°-α=90°-60°=30°．
故答案为：30°
根据折射定律得n=
| sinr |
| sini |
| 2 |
| ||
| 2 |
同理可知，第二条出射光线的折射角也是45°，
从图中的四边形可求出α=360°-120°-90°-90°=60°，
β=360°-135°-135°-α=90°-60°=30°．
故答案为：30°
点评：本题解题的关键是作出光路图，运用几何知识和折射定律相结合进行求解．
练习册系列答案
相关题目
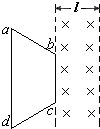（2005?山东）如图所示，两条平行虚线之间存在匀强磁场，虚线间的距离为l，磁场方向垂直纸面向里，abcd是位于纸面内的梯形线圈，ad与bc间的距离也为l，t=0时刻，bc边与磁场区域左边界重合．现令线圈以向右的恒定速度v沿垂直于磁场区域边界的方向穿过磁场区域，取沿a→b→c→d→a方向的感应电流为正，则在线圈穿越磁场区域的过程中，感应电流I随时间t变化的图线是（ ）
如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为l=0.2m，在导轨的一端接有阻值为R=0.5Ω的电阻，在X≥0处有一与水平面垂直的均匀磁场，磁感强度B=0.5T．一质量为m=0.1kg的金属直杆垂直放置在导轨上，并以v0=2m/s的初速度进人磁场，在安培力和一垂直于杆的水平外力 F的共同作用下作匀变速直线运动，加速度大小为a=2m/s2，方向与初速度方向相反．设导轨和金属杆的电阻都可以忽略，且接触良好，求：
如图所示，两条间距l=1m的光滑金属导轨制成倾角37°的斜面和水平面，上端用阻值为R=4Ω的电阻连接．在斜面导轨区域和水平导轨区域内分别有垂直于斜面和水平面的匀强磁场B1 和B2，且B1=B2=0.5T．ab和cd是质量均为m=0.1kg，电阻均为r=4Ω的两根金属棒，ab置于斜面导轨上，cd置于水平导轨上，均与导轨垂直且接触良好．已知t=0时刻起，cd棒在外力作用下开始水平向右运动（cd棒始终在水平导轨上运动），ab棒受到F=0.6-0.2t（N）沿斜面向上的力作用，处于静止状态．不计导轨的电阻，试求：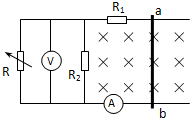
如图所示，两条平行的光滑水平导轨上，用套环连着一质量为0.2kg、电阻为2Ω的导体杆ab，导轨间匀强磁场的方向垂直纸面向里．已知R1=3Ω，R2=6Ω，电压表的量程为0～10V，电流表的量程为0～3A（导轨的电阻不计）．求：