��Ŀ����
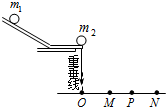
��ͼ��ʾΪ����֤��ײ�еĶ����غ㡱��ʵ��װ�ã�
��1������˵�����ϱ�ʵ��Ҫ�����______��
A��������Ȱ������������С����
B��ÿ������������ͬһ�߶��ɾ�ֹ�ͷ�
C����װ���ʱĩ�����߱���ˮƽ
D��ʵ������Ҫ�������ĩ�������ĸ߶�
��2��ʵ���м�¼�˹��ĩ���ڼ�¼ֽ�ϵ���ֱͶӰΪO�㣬������ͷ��������ڼ�¼ֽ���ҵ��������ƽ�����λ��M��P��N����������ǵ�O��ľ���ֱ�Ϊ
��
��
����֪�����������Ϊm1�����������Ϊm2��ֻҪ��֤��ʽ______������������Ϊ��ײ�еĶ����غ㣮
��3�����㣨2��������£��������ʽ______������������Ϊ��ײΪ������ײ��������
��
��
��ʾ��
��1������˵�����ϱ�ʵ��Ҫ�����______��
A��������Ȱ������������С����
B��ÿ������������ͬһ�߶��ɾ�ֹ�ͷ�
C����װ���ʱĩ�����߱���ˮƽ
D��ʵ������Ҫ�������ĩ�������ĸ߶�
��2��ʵ���м�¼�˹��ĩ���ڼ�¼ֽ�ϵ���ֱͶӰΪO�㣬������ͷ��������ڼ�¼ֽ���ҵ��������ƽ�����λ��M��P��N����������ǵ�O��ľ���ֱ�Ϊ
| . |
| OM |
| . |
| OP |
| . |
| ON |
��3�����㣨2��������£��������ʽ______������������Ϊ��ײΪ������ײ��������
| . |
| OM |
| . |
| OP |
| . |
| ON |

��1��A��Ϊ��ֹ����m1������������������Ҫ���ڱ�������������m1��m2����A����
B��Ϊ��֤��ײ�ij��ٶ���ͬ��������ÿ�α���ӹ����ͬһλ���ɾ�ֹ���£���B��ȷ��
C��Ϊ��֤С����ƽ���˶�����װ���ʱĩ�����߱���ˮƽ����C��ȷ��
D��С����ƽ���˶���ʱ���ɸ߶Ȳ���������ڸ߶Ȳ�һ������ƽ��ʱ�䶼��ͬ����ˮƽ�����ƽ�ij��ٶȳ����ȣ��ʲ���Ҫ�����߶ȲֻҪ����m1
=m1
+m2
����һ����m1v1+m2v2=m1v1��+m2v2�䣬��D����
��ѡ��BC��
��2��ʵ��Ҫ��֤����С����ײǰ���ܶ����غ㣬����m1v1+m2v2=m1v1��+m2v2�䣻
С����ƽ���˶���ʱ���ɸ߶Ȳ���������ڸ߶Ȳ�һ������ƽ��ʱ�䶼��ͬ����ˮƽ�����ƽ�ij��ٶȳ����ȣ��ʲ���Ҫ�����߶ȲֻҪ���㣺m1
=m1
+m2
��
��3��С����������ײ����ײ������ϵͳ�����غ㡢��е��Ҳ�غ㣬�����غ㶨�ɣ��У�
m1
=m1
+m2
m1
2=
m1
2+
m2
2
��ʽ������ȥ�����ɵã�
2=
2+
?
�ٻ���õ���
=
+
�ʴ�Ϊ����1��BC����2��m1
=m1
+m2
����3��
=
+
��
B��Ϊ��֤��ײ�ij��ٶ���ͬ��������ÿ�α���ӹ����ͬһλ���ɾ�ֹ���£���B��ȷ��
C��Ϊ��֤С����ƽ���˶�����װ���ʱĩ�����߱���ˮƽ����C��ȷ��
D��С����ƽ���˶���ʱ���ɸ߶Ȳ���������ڸ߶Ȳ�һ������ƽ��ʱ�䶼��ͬ����ˮƽ�����ƽ�ij��ٶȳ����ȣ��ʲ���Ҫ�����߶ȲֻҪ����m1
| . |
| OP |
| . |
| OM |
| . |
| ON |
��ѡ��BC��
��2��ʵ��Ҫ��֤����С����ײǰ���ܶ����غ㣬����m1v1+m2v2=m1v1��+m2v2�䣻
С����ƽ���˶���ʱ���ɸ߶Ȳ���������ڸ߶Ȳ�һ������ƽ��ʱ�䶼��ͬ����ˮƽ�����ƽ�ij��ٶȳ����ȣ��ʲ���Ҫ�����߶ȲֻҪ���㣺m1
| . |
| OP |
| . |
| OM |
| . |
| ON |
��3��С����������ײ����ײ������ϵͳ�����غ㡢��е��Ҳ�غ㣬�����غ㶨�ɣ��У�
m1
| . |
| OP |
| . |
| OM |
| . |
| ON |
| 1 |
| 2 |
| . |
| OP |
| 1 |
| 2 |
| . |
| OM |
| 1 |
| 2 |
| . |
| ON |
��ʽ������ȥ�����ɵã�
| . |
| OP |
| . |
| OM |
| . |
| ON |
| . |
| MP |
�ٻ���õ���
| . |
| ON |
| . |
| OP |
| . |
| OM |
�ʴ�Ϊ����1��BC����2��m1
| . |
| OP |
| . |
| OM |
| . |
| ON |
| . |
| ON |
| . |
| OP |
| . |
| OM |

��ϰ��ϵ�д�
 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
�����Ŀ