题目内容
（10分）如图所示，在水平向右的匀强电场中，一长为L的绝缘轻杆，一端固定于O点，杆可绕O点在竖直平面内转动。杆的另一端连接一质量为m的带正电小球，小球受到的电场力是重力的
倍，要使小球能在竖直平面内做圆周运动，则小球经过最高点的速度最小为多少？
解析:这是一个复合场问题：重力场与电场的复合场，我们最习惯于研究重力场中的竖直平面内的圆周运动，我们就把复合场类比于重力场进行解题，首先确定复合场方向即小球的平衡位置。受力分析知，小球的平衡位置为与竖直方向夹角30°，复合场的等效成重力场的等效加速度为
,如下图A点是平衡位置，B点是等效重力场中的最高点，C点是几何上最高点，也就是我们要求的最高点。
因为是杆子所以B点的最小速度为0，再在BC间用动能定理可求得C点的速度；或类比于重力场中的运动进行计算，最后只需将g改成即可。小球经过最高点的速度最小为
错解分析:错解一：忽略电场的作用，直接应用结论，小球在最高点的最小速度为0。
错解二：不知杆与绳的区别，不会用合场的思想类比重力场进行解题，错解答案较多。
练习册系列答案
相关题目
如图所示，在水平向右的匀强电场中，用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点，平衡时，小球位于B点，此时绳与竖直方向的夹角为θ（θ＜45°）．已知重力加速度为g．求：
如图所示，在水平向右的拉力F作用下，木块在长木板上向右做匀减速直线运动，加速度大小为a．长木板处于静止状态．已知，木块质量为m，长木板质量为M，长木板与水平地面间的动摩擦因数为μ1，木块与长木板间的动摩擦因数为μ2．地面对长木板的摩擦力大小为（ ）
如图所示，在水平向右的匀强电场中，用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点，平衡时，小球位于B点，此时绳与竖直方向的夹角为θ（θ＜45°）．已知重力加速度为g．求：小球静止在B点时受到绳的拉力大小．
如图所示，在水平向右场强为E的匀强电场中，有一质量为m、电荷量为+q的点电荷从A点由静止释放，在电场力的作用下经时间t运动到B点．求：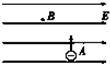
如图所示，在水平向右的匀强电场中的A点，有一个质量为m、带电荷量为-q的油滴以速度v竖直向上运动．已知当油滴经过最高点B时，速度大小也为v．求：