Question

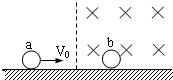如图所示，在光滑的绝缘水平面上，有直径相同的两个金属球a和b，质量分别为m_a=2m，m_b=m，b球带正电荷2q，静止在磁感强度为B的匀强磁场中．原来不带电的a球以速度V₀进入磁场与b球发生正碰．若碰后b球对桌面压力恰好为零，求a球对桌面压力是多大？

Answer 1

分析：a和b碰撞前后动量守恒，且碰后两球均分电荷，都将受到洛伦兹力，由左手定则判断洛伦兹力的方向，即可求解．

解答：解：a球匀速进入磁场与b球相碰，满足动量守恒，且碰后a、b的带电量均为q，设碰后a、b的速度分别为v_a，v_b，规定向右为正方向，依动量守恒定律有：
m_av₀=m_av_a+m_bv_b
对b球：qBv_b=m_bg
m_a=2m_b=2m
解得：v_a=v₀-

mg

2Bq

对球a：F_N=m_ag-qBv_a=

5

2

mg-qv₀B
由牛顿第三定律有：F_N=-F′_N
故a球对水平面的压力为

5

2

mg-qv₀B
答：碰后a对水平地面的压力为

5

2

mg-qv₀B．

点评：抓住碰撞前后动量守恒，且碰后两球均带正电，都受洛伦兹力，同时注意挖掘隐含条件：碰后b球对桌面压力恰好为零，洛伦兹力等于其重力．