Question

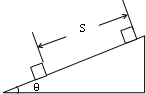18世纪的瑞士著名科学家欧拉（L．Euler）首先采用使物体做加速运动的方法测定物体的动摩擦因数，实验装置如图所示．在一个倾角为θ的斜面上，使一小木块从静止开始加速下滑．测出时间t内小木块的位移s，即可用t、s和θ得出动摩擦因数的表达式．请推导这个表达式．

Answer 1

分析：根据匀变速直线运动的位移时间公式求出加速度的大小，结合牛顿第二定律求出动摩擦因数的表达式．

解答：解：滑块受到三个力：重力mg、垂直于斜面向上的支持力F_N、沿斜面向上的滑动摩擦力f．
由牛顿第二定律得：mgsinθ-μmgcosθ=ma   ①
由运动学公式得：s=

1

2

at2   ②
由①②得到：μ=tanθ-

2s

t2gcosθ

答：动摩擦因数的表达式为μ=tanθ-

2s

t2gcosθ

．

点评：本题考查了牛顿第二定律和运动学公式的综合，知道加速度是联系力学和运动学的桥梁．