题目内容
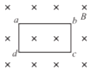
【题目】如图所示,在宽度均为![]() m的两个相邻的、足够长的条形区域内分别有匀强磁场和匀强电场,磁场的磁感应强度大小B=3T,方向垂直于纸面向里,电场方向与电、磁场分界线平行向右.一质量为m=3×10-10㎏、电荷量q=5×10-6C的带正电粒子以大小
m的两个相邻的、足够长的条形区域内分别有匀强磁场和匀强电场,磁场的磁感应强度大小B=3T,方向垂直于纸面向里,电场方向与电、磁场分界线平行向右.一质量为m=3×10-10㎏、电荷量q=5×10-6C的带正电粒子以大小![]() =1×104的速度从磁场区域上边界的P点与边界成θ=30°角斜射入磁场,最后从电场下边界上的Q点射出,已知P、Q连线垂直于电场方向,不计粒子重力,求:
=1×104的速度从磁场区域上边界的P点与边界成θ=30°角斜射入磁场,最后从电场下边界上的Q点射出,已知P、Q连线垂直于电场方向,不计粒子重力,求:

(1)粒子在磁场中的运动的时间;
(2)匀强电场的电场强度的大小.
【答案】(1)![]() s (2)
s (2)![]() N/C
N/C
【解析】
试题(1)作出粒子在磁场中运动的轨迹图,根据几何关系求出偏转角,即可求解在磁场中运动的时间;(2)粒子在电场中做类平抛运动,根据类平抛运动的规律即可求出电场强度.
(1)粒子在磁场中运动的轨迹图如图所示:

粒子在磁场中做匀速圆周运动,洛仑兹力提供向心力:![]()
解得:r=0.2m
过P点做射入速度方向的垂线,由几何关系可知,粒子在磁场中做圆周运动的轨迹对应的圆心恰好在磁场的下边界上,则粒子垂直磁场下边界射入电场,粒子在磁场中做圆周运动所对应的圆心角为![]()
所以粒子在磁场中的时间:![]()
(2)粒子在电场中做类平抛运动,则有:
沿电场方向:![]()
垂直电场方向:![]() ,其中
,其中![]()
解得:![]()

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目