题目内容
 如图所示,木块A的质量为m,木块B的质量为M,叠放在光滑的水平面上.现用水平力F作用于A,恰能使A、B一起运;今撤去力F,将另一水平F′作用于木块B,则保持A、B相对静止的条件是F′不超过( )
如图所示,木块A的质量为m,木块B的质量为M,叠放在光滑的水平面上.现用水平力F作用于A,恰能使A、B一起运;今撤去力F,将另一水平F′作用于木块B,则保持A、B相对静止的条件是F′不超过( )分析:当水平力为F时,运用整体隔离法求出A、B间的最大静摩擦力,当施加F′时,抓住A、B间的静摩擦力小于等于最大静摩擦力,运用牛顿第二定律求出F′满足的条件.
解答:解:系统在水平方向上只受力F作用,恰能一起运动,则A、B具有相同的加速度,即a=
,木块B水平方向上只受A对B的静摩擦力,因此最大静摩擦力fm=Ma;若撤去F.将水平力F′作用于B,则对系统有a′=
,木块A在水平方向上只受B对A的静摩擦力f,相对静止的条件是相互作用的静摩擦力f≤fm,且f=ma′.
联立解得F′≤
F.故C正确,A、B、D错误.
故选C.
| F |
| M+m |
| F′ |
| m+M |
联立解得F′≤
| M |
| m |
故选C.
点评:解决本题的关键能够正确地受力分析,抓住临界状态,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
相关题目
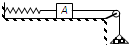 如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )
如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )


