题目内容
如图所示，在光滑的水平地面上，静止着质量为M =2.0kg的小车A，小车的上表面距离地面的高度为0.8m，小车A的左端叠放着一个质量为m=1.0kg的小物块B（可视为质点）处于静止状态，小物块与小车上表面之间的动摩擦因数μ=0.20。在小车A的左端正上方，用长为R=1.6m的不可伸长的轻绳将质量为m =1.0kg的小球C悬于固定点O点。现将小球C拉至使轻绳拉直且与竖起方向成θ=60°角的位置由静止释放，到达O点的正下方时，小球C与B发生弹性正碰（碰撞中无机械能损失），小物块从小车右端离开时车的速度为1m/s，空气阻力不计，取g=10m/s2． 求：
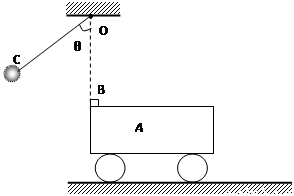
（1）小车上表面的长度L是多少?
（2）小物块落地时距小车右端的水平距离是多少?
（1）
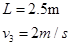（2）
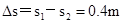
【解析】解：（1）静止释放后小球做圆周运动到最低点过程，由机械能守恒定律得
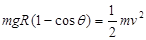（2分）
解得v=4m/s （1分）
小球C与B碰撞过程中动量守恒和机械能保持不变，则
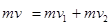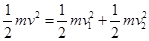（1分）
（1分）
解得：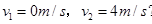
（1分）
B在小车A上滑动，系统动量守恒，设B滑到A最右端时速度为v3，车速为v4则
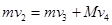（2分）
B在小车A上滑动的过程中，系统减小的机械能转化为内能，由能量守恒定律得
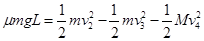（2分）
联立解得：
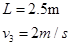（2分）
(2)滑块离开A后将做平抛运动，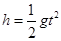
（1分）
小滑块到地面所需的时间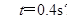
对应的小物块水平位移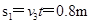
小车滑行的位移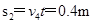
小物块距小车右端的水平距离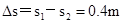
（1分）
本题考查的是对动量守恒问题与机械能守恒的问题的应用问题，根据机械能守恒定律和动量守恒定律可以计算小球和滑块的速度，再利用能量守恒可以计算机械能的损失即摩擦力做功，再利用平抛运动的规律计算出水平距离；
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别挂上小球C和物体B，在B的下端再挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时圆周运动的半径为R，现剪断连接A、B的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，一根不可伸长的轻绳穿过小孔．绳的两端分别拴有一小球C和一质量为m的物体B，在物体B的下端还悬挂有一质量为3m的物体A．使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动的半径为R．现剪断连接A、B的绳子，稳定后，小球以2R的半径在水平面上做匀速圆周运动，则下列说法正确的（ ）
如图所示，在光滑的水平板的中央有一光滑的小孔，用不可伸长的轻绳穿过小孔，绳的两端分别栓上一小球C和一物体B，在B的下端再悬挂一重物A，现使小球C在水平板上以小孔为圆心做匀速圆周运动，稳定时，圆周运动半径为R．现剪断连接AB的绳子，稳定后，小球以另一半径在水平面上做匀速圆周运动，则下列说法正确的是（ ）
