题目内容
 (2009?湖北模拟)如图所示,在倾角为θ的固定光滑斜面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,C为一固定的挡板,小店让一质量为m的物体D从距A为L的位置由静止释放,D和A相碰后立即粘为一体,之后在斜面上做简谐运动,在简谐运动过程中,物体B对C的最小弹力为
(2009?湖北模拟)如图所示,在倾角为θ的固定光滑斜面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,C为一固定的挡板,小店让一质量为m的物体D从距A为L的位置由静止释放,D和A相碰后立即粘为一体,之后在斜面上做简谐运动,在简谐运动过程中,物体B对C的最小弹力为| 1 |
| 2 |
分析:当AD受力平衡时,AD处于平衡位置,由胡克定律可求得平衡位置时弹簧的形变量;再由B对C的最小弹力可求得AD能达到的最大位移,即可求得振幅;由简谐运动的对称性可求得最大弹力.
解答:解:当弹力等于AD的重力的分力时AD处于平衡状态,由kx=2mgsinθ可知,平衡位置时弹簧的形变量为x0=
,处压缩状态;
当B对C弹力最小时,对B分析,则有mgsinθ=Kx+
mgsinθ;
故弹簧应伸长达最大位移处,此时形变量x=
,此时弹簧处于伸长状态;
故简谐运动的振幅为A=x+x0=
+
=
;故B正确,A错误;
当AD运动到最低点时,B对C的弹力最大;由对称性可知,此时弹簧的形变量为A+x0=
+
=
;
此时弹力为F=k(A+x0)=
;
B对C的弹力为F+mgsinθ=
;故C错误,D正确;
故选BD.
| 2mgsinθ |
| k |
当B对C弹力最小时,对B分析,则有mgsinθ=Kx+
| 1 |
| 2 |
故弹簧应伸长达最大位移处,此时形变量x=
| mgsinθ |
| 2k |
故简谐运动的振幅为A=x+x0=
| 2mgsinθ |
| k |
| mgsinθ |
| 2k |
| 5mgsinθ |
| 2k |
当AD运动到最低点时,B对C的弹力最大;由对称性可知,此时弹簧的形变量为A+x0=
| 5mgsinθ |
| 2k |
| 2mgsinθ |
| k |
| 9mgsinθ |
| 2k |
此时弹力为F=k(A+x0)=
| 9mgsinθ |
| 2 |
B对C的弹力为F+mgsinθ=
| 11mgsinθ |
| 2k |
故选BD.
点评:本题关键在于找出简谐运动的平衡位置,从而确定出物体的振幅及回复力.

练习册系列答案
相关题目
 (2009?湖北模拟)如图所示,可视为点电荷的小物块A、B分别带负电和正电,B固定,其正下方的A静止在绝缘斜面上,则A受力个数可能为( )
(2009?湖北模拟)如图所示,可视为点电荷的小物块A、B分别带负电和正电,B固定,其正下方的A静止在绝缘斜面上,则A受力个数可能为( ) (2009?湖北模拟)如图所示,物体A贴在竖直墙面上,在竖直轻弹簧作用下,A、B保持静止.则物体A的受力个数为( )
(2009?湖北模拟)如图所示,物体A贴在竖直墙面上,在竖直轻弹簧作用下,A、B保持静止.则物体A的受力个数为( )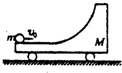 (2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )
(2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )