Question

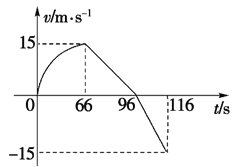
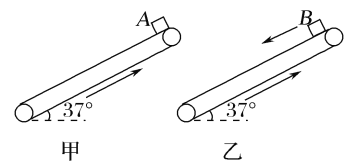
【题目】甲、乙两传送带倾斜放置，与水平方向夹角均为37°，传送带乙长为4 m，传送带甲比乙长0.45 m，两传送带均以3 m/s的速度逆时针匀速转动，可视为质点的物块A从传送带甲的顶端由静止释放，可视为质点的物块B由传送带乙的顶端以3 m/s的初速度沿传送带下滑，两物块质量均为2kg，与传送带间的动摩擦因数均为0.5，取g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8。求：

(1)物块A由传送带顶端滑到底端经历的时间；

(2)物块A、B在传送带上的划痕长度之比。

(3)物块A、B与传送带因摩擦产生的热量分别是多少。

Answer 1

【答案】（1） （2） （3）11.6J；

【解析】

(1)对物块A由牛顿第二定律知

代入数值得：

设经时间物块与传送带共速，则由运动学规律知：

即：

此过程中物块的位移为：

物块与传送带共速后，由牛顿第二定律知：

代入数值得：

由运动学规律知：

甲

代入数值得：

所以物块由传送带顶端滑到底端经历的时间为：

(2)在物块的第一个加速过程中，物块在传送带上的划痕长度为：

在物块的第二个加速过程中，物块在传送带上的划痕长度为：

所以物块在传送带上的划痕长度为

由分析知物块的加速度与物块A在第二个加速过程的加速度相同，从传送带顶端加速到底端所需时间与相同

所以物块在传送带上的划痕长度为：

故物块、在传送带上的划痕长度之比为：

(3)物块的摩擦生热：

物块的摩擦生热：