题目内容
如图所示，AD、BD、CD都是光滑的直角斜面，斜面固定在水平地面上，现使一小物体分别从A、B、C点由静止开始下滑到D点，所用时间分别为t1、t2、t3，则（ ）A．t2＜t1＞t3
B．t3＞t2＞t1
C．t2＜t1=t3
D．t1＞t2＞t3
【答案】分析：先受力分析后根据牛顿第二定律计算出小物体沿任意一斜面滑动的加速度，然后根据位移时间关系公式计算出时间，对表达式分析，得出时间与各因素的关系后得出结论．
解答：解：对小物块，受重力和支持力，将重力沿杆的方向和垂直杆的方向正交分解，
根据牛顿第二定律得小物块做初速为零的匀加速直线运动的加速度为a=gcosθ（θ为斜面与竖直方向的夹角）
设水平方向直角边长为s，由图中的直角三角形可知，小物块的位移x=
根据x=
得：
t=
=
带入角度可知：t1=
，t2=
，t3=
故t1=t3＞t2，
故选C．
点评：本题关键从众多的杆中抽象出一根杆，假设其与水平方向的夹角为θ，然后根据牛顿第二定律求出加速度，再根据运动学公式求出时间表达式讨论．
解答：解：对小物块，受重力和支持力，将重力沿杆的方向和垂直杆的方向正交分解，
根据牛顿第二定律得小物块做初速为零的匀加速直线运动的加速度为a=gcosθ（θ为斜面与竖直方向的夹角）
设水平方向直角边长为s，由图中的直角三角形可知，小物块的位移x=
根据x=
得：t=
=带入角度可知：t1=
，t2=，t3=故t1=t3＞t2，
故选C．
点评：本题关键从众多的杆中抽象出一根杆，假设其与水平方向的夹角为θ，然后根据牛顿第二定律求出加速度，再根据运动学公式求出时间表达式讨论．
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
（2004?江西）如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示滑环到达d所用的时间，则（ ）
（2011?甘肃二模）如图所示，AD、BD、CD都是光滑的直角斜面，斜面固定在水平地面上，现使一小物体分别从A、B、C点由静止开始下滑到D点，所用时间分别为t1、t2、t3，则（ ）
如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点．每根杆上都套着一个完全相同的小滑环（图中未画出），三个滑环分别从a、b、c点无初速释放，关于它们下滑过程的下列说法中正确的是（ ）
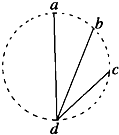如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周，a点为圆周的最高点，d为圆周的最低点．每根杆上都套着一个质量相同的小滑环（图中未画出），三个滑环分别a、b、c处释放（初速度为零），关于它们下滑的过程，下列说法中正确的是（ ）| A、重力对它们的冲量相同 | B、弹力对它们的冲量相同 | C、合外力对它们的冲量相同 | D、它们的动能增量相同 |
如图所示，ad、bd、 cd是竖直面内的三根固定的光滑细杆，a、ｂ、c、ｄ位于同一圆周上，ａ点为圆周上最高点，ｄ点为圆周上最低点。每根杆上都套有一个小圆环，三个圆环分别从ａ、ｂ、c处由静止释放，用t1 、t2、t3依次表示各环到达d点所用的时间，则（ ）
| A．t 1＜t2＜ t3 | B．t 1＞t2＞ t3 |
| C．t 3＞t1＞ t2 | D．t 1＝t2＝t3 |