Question

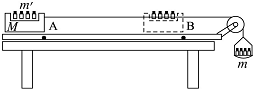某同学设计了如图所示的装置，利用米尺、秒表、轻绳、轻滑轮、轨道、滑块、托盘和砝码等器材来测定滑块和轨道间的动摩擦因数μ．滑块和托盘上分别放有若干砝码，滑块质量为M．滑块上砝码总质量为m’，托盘和盘中砝码的总质量为m．实验中，滑块在水平轨道上从A到B做初速度为零的匀加速直线运动，重力加速度为g．
（1）根据牛顿运动定律得到滑块加速度a与m的关系为：

 

；
（2）他想通过多次改变m，测出相应的a值，并利用上式来计算μ．若要求a是m的一次函数，必须使上式中的

 

保持不变，实验中应将从托盘中取出的砝码置于

 

．

Answer 1

分析：（1）先对托盘和盘中砝码受力分析，受重力和拉力，根据牛顿第二定律列式；再对滑块和滑块上砝码整体受力分析，受重力、支持力、拉力和滑动摩擦力，根据牛顿第二定律再次列式；最后联立求解得到a与m的关系式；
（2）根据上问中的函数表达式进行分析即可．

解答：解：（1）先对托盘和盘中砝码受力分析，受重力和拉力，根据牛顿第二定律，有：
mg-T=ma                                     ①
再对滑块和滑块上砝码整体受力分析，受重力、支持力、拉力和滑动摩擦力，根据牛顿第二定律，有：
T-（M+m′）g=（M+m′）a                       ②
联立①②解得：
a=

mg-μ(m′+M)g

m+m′+M

=

(1+μ)g

m+m′+M

m-μg               ③
（2）若要求a是m的一次函数，必须使上式中的

(1+μ)g

m+m′+M

一定，即m′+m保持不变即可；
故可以将从托盘中取出的砝码置于滑块上；
故答案为：（1）a=

(1+μ)g

m+m′+M

m-μg；（2）m′+m，滑块上．

点评：本题根据先根据牛顿第二定律并结合隔离法求解出加速度的表达式，然后再进行分析讨论，不难．