题目内容
在质量为M的电动机飞轮上固定着一个质量为m的重物，它到转轴的距离为r，为使电动机不从地面跳起，则电动机的飞轮角速度不得超过 ，若以上述角速度匀速转动，它对地面的最大压力为 ．
【答案】分析：当重物转到最高点时，对电动机的拉力等于电动机的重力时，电动机恰好不从地面跳起，此时电动机的飞轮角速度是电动机不从地面跳起时最大的角速度，以重物为研究对象，根据牛顿第二定律求解此角速度．当以此角速度匀速转动，重物转到最低点时，电动机对地面的压力最大，再由牛顿运动定律求解电动机对地面最大的压力．
解答：解：设电动机恰好不从地面跳起时飞轮角速度是ω．此时电动机对重物的作用力F=Mg．以重物为研究对象，根据牛顿第二定律得
mg+F=mω2r
得到ω=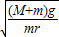
若以上述角速度匀速转动，重物转到最低点时，则有
F′-mg=mω2r，得到F′=mg+mω2r=mg+（M+m）g=（M+2m）g
根据牛顿第三定律得，重物对电动机压力大小为则对地面的最大压力为Mg+（M+2m）g=2（M+m）g．
故答案为：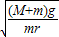
，2（M+m）g．
点评：本题首先要选择研究对象，分析受力情况．其次确定电动机恰好不从地面跳起的临界条件．
解答：解：设电动机恰好不从地面跳起时飞轮角速度是ω．此时电动机对重物的作用力F=Mg．以重物为研究对象，根据牛顿第二定律得
mg+F=mω2r
得到ω=
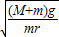
若以上述角速度匀速转动，重物转到最低点时，则有
F′-mg=mω2r，得到F′=mg+mω2r=mg+（M+m）g=（M+2m）g
根据牛顿第三定律得，重物对电动机压力大小为则对地面的最大压力为Mg+（M+2m）g=2（M+m）g．
故答案为：
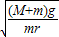，2（M+m）g．点评：本题首先要选择研究对象，分析受力情况．其次确定电动机恰好不从地面跳起的临界条件．
练习册系列答案
相关题目
在如图所示电路中，闭合开关S．请回答下列问题：
算获胜．已知滑板与墙顶部平面的动摩擦因数为μ0，滑板与人的总质量为M，滑块到达圆弧形轨道底端时对轨道的压力大小为F，重力加速度为g，不计滑板的长度，运动员可视为质点．求：
=37°。求
=37°。求
=37°。求