��Ŀ����
�ڡ���֤��е���غ㶨�ɡ���ʵ���У�����Ϊm���ش��Ӹߴ��ɾ�ֹ��ʼ���䣬�ش������ŵ�ֽ��ͨ������ʱ�������һϵ�еĵ㣬��ֽ���ϵĵ㼣���в����Ϳ�����֤��е���غ㶨�ɣ�
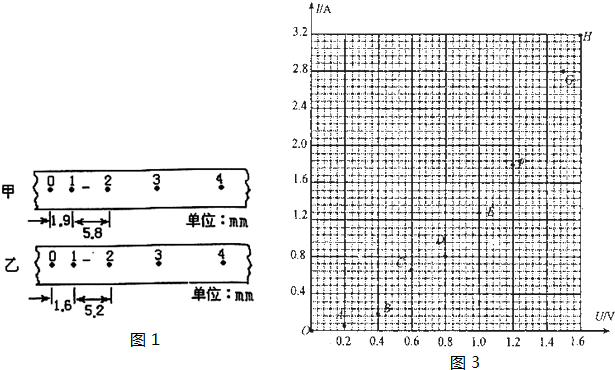
��1����ͼ��ʾ��ѡȡֽ����������������A��B��C��D��E�����A�����ʼ��O�ľ���ΪS0��������ͼ��ʹ�õ�Դ��Ƶ��Ϊf��Ƶ��Ϊ���ڵĵ����������C��ʱ������ٶ�Ϊ
������ʱ���ڴ�C��ʱ�ش��Ķ���Ϊ
mf2(s1+s2)2
mf2(s1+s2)2������ʱ���ڴ�O���C������ʱ�����ش��������ܵļ�����Ϊ

��2��ʵ���з����ش����ٵ����������Դ����ش����ӵĶ��ܣ���ԭ����Ҫ����Ϊ���ش�����ֽ������Ĺ����д������������ã�����֪�����������ٶȵ�ֵΪg���ã�1��С�⼰��Ŀ�и�������֪����ʾ�ش�������������ܵ���ƽ��������СΪ
��1����ͼ��ʾ��ѡȡֽ����������������A��B��C��D��E�����A�����ʼ��O�ľ���ΪS0��������ͼ��ʹ�õ�Դ��Ƶ��Ϊf��Ƶ��Ϊ���ڵĵ����������C��ʱ������ٶ�Ϊ
| (s1+s2)f |
| 4 |
| (s1+s2)f |
| 4 |
| 1 |
| 32 |
| 1 |
| 32 |
mg��s0+s1��
mg��s0+s1��
��
��2��ʵ���з����ش����ٵ����������Դ����ش����ӵĶ��ܣ���ԭ����Ҫ����Ϊ���ش�����ֽ������Ĺ����д������������ã�����֪�����������ٶȵ�ֵΪg���ã�1��С�⼰��Ŀ�и�������֪����ʾ�ش�������������ܵ���ƽ��������СΪ
mg-
mf2
| 1 |
| 32 |
| (s1+s2)2 |
| s0+s1 |
mg-
mf2
��| 1 |
| 32 |
| (s1+s2)2 |
| s0+s1 |
���������ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ���������������������ݴ����Լ�ע�����
֪����Դ��Ƶ��Ϊf���������������ڣ�
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ��Ӷ�������ܣ����ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
���������ܼ�С���Ͷ�����������֪������£�����Ӧ�����ö��ܶ������������С��
������ĸ����Ҫϸ�ģ�
֪����Դ��Ƶ��Ϊf���������������ڣ�
ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ��Ӷ�������ܣ����ݹ��ܹ�ϵ���������ܼ�С������������������ֵ��
���������ܼ�С���Ͷ�����������֪������£�����Ӧ�����ö��ܶ������������С��
������ĸ����Ҫϸ�ģ�
����⣺��1�������ȱ���ֱ���˶�������
vC=
=
=
���ݶ��ܶ���ʽ�ã�
��C��ʱ�ش��Ķ���ΪEkC=
mvC2=
mf2(s1+s2) 2
�ش����ܵ�������Ϊ��EK=EkC-0=
mf2(s1+s2) 2
�������ܼ�С����Ep=mgh=mg��s0+s1��
��2���������������������mg������f��
���ݶ��ܶ����о������0��C�ã�
w��=��Ek ������������������������������
mgh-fh=EkC-0
f=mg-
=mg-
mf2
�ʴ�Ϊ��
��1��
��
mf2(s1+s2) 2��mg��s0+s1��
��2��mg-
mf2
vC=
| xAE |
| tAE |
| s1+s2 |
| 4T |
| (s1+s2)f |
| 4 |
���ݶ��ܶ���ʽ�ã�
��C��ʱ�ش��Ķ���ΪEkC=
| 1 |
| 2 |
| 1 |
| 32 |
�ش����ܵ�������Ϊ��EK=EkC-0=
| 1 |
| 32 |
�������ܼ�С����Ep=mgh=mg��s0+s1��
��2���������������������mg������f��
���ݶ��ܶ����о������0��C�ã�
w��=��Ek ������������������������������
mgh-fh=EkC-0
f=mg-
| EKC |
| h |
| 1 |
| 32 |
| (s1+s2)2 |
| s0+s1 |
�ʴ�Ϊ��
��1��
| (s1+s2)f |
| 4 |
| 1 |
| 32 |
��2��mg-
| 1 |
| 32 |
| (s1+s2)2 |
| s0+s1 |
������ֽ������Ĵ�������ѧʵ���г��������⣮���ǿ���ֽ����ʵ���У���ֽ���ȱ���ֱ���˶������ֽ���ϵĵ��࣬�����ȱ���ֱ���˶������ۣ��ɼ�������ij��ʱֽ���˶���˲ʱ�ٶȺͼ��ٶȣ�
���ܶ�����Ӧ�÷�Χ�ܹ㣬�ڱ��������ƽ��������
���ܶ�����Ӧ�÷�Χ�ܹ㣬�ڱ��������ƽ��������

��ϰ��ϵ�д�
 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
�����Ŀ
 ��2010?�ɶ���ģ����1������֤����е���غ㶨�ʡ��������У�
��2010?�ɶ���ģ����1������֤����е���غ㶨�ʡ��������У�
